Find the transfer function from force u to posi- tion y Y
Elements Of Electromagnetics
7th Edition
ISBN:9780190698614
Author:Sadiku, Matthew N. O.
Publisher:Sadiku, Matthew N. O.
ChapterMA: Math Assessment
Section: Chapter Questions
Problem 1.1MA
Related questions
Question
When I do the work, I come up with the same answer as choice c. I just want to make sure and double check my work. Thanks!

Transcribed Image Text:**Problem Statement:**
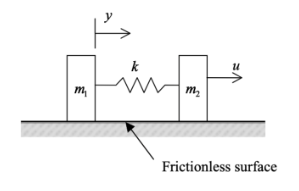
Find the transfer function \(\frac{Y(s)}{U(s)}\) from force \(u\) to position \(y\).
**Diagram Explanation:**
The diagram shows a mechanical system consisting of two masses, \(m_1\) and \(m_2\), connected by a spring with spring constant \(k\). Mass \(m_2\) is subject to an external force \(u\). The system is placed on a frictionless surface, allowing the masses to move freely.
**Options:**
(a) \(\frac{m_1 s^2 + k}{m_1 m_2 s^4 + (km_1 + km_1)s^2 + k^2}\)
(b) \(\frac{m_1 s^2 + k}{m_1 m_2 s^4 + (km_1 + km_1)s^2}\)
(c) \(\frac{k}{m_1 m_2 s^4 + (km_1 + km_2)s^2}\)
(d) \(\frac{k}{m_1 m_2 s^4 + (km_1 + km_1)s^2 + k^2}\)
(e) none of the above
**Solution Explanation:**
To solve for the transfer function \(\frac{Y(s)}{U(s)}\), one must analyze the system's dynamics, derive the equations of motion for the masses, and convert them into the Laplace domain. The correct expression relates the force \(u\) to the position \(y\) through these equations, considering the spring dynamics and the inertias of both masses involved.
Expert Solution
Step 1: Write the given data and what is to find
Given:
To find:
Transfer function .
Step by step
Solved in 5 steps with 8 images

Recommended textbooks for you

Elements Of Electromagnetics
Mechanical Engineering
ISBN:
9780190698614
Author:
Sadiku, Matthew N. O.
Publisher:
Oxford University Press

Mechanics of Materials (10th Edition)
Mechanical Engineering
ISBN:
9780134319650
Author:
Russell C. Hibbeler
Publisher:
PEARSON

Thermodynamics: An Engineering Approach
Mechanical Engineering
ISBN:
9781259822674
Author:
Yunus A. Cengel Dr., Michael A. Boles
Publisher:
McGraw-Hill Education

Elements Of Electromagnetics
Mechanical Engineering
ISBN:
9780190698614
Author:
Sadiku, Matthew N. O.
Publisher:
Oxford University Press

Mechanics of Materials (10th Edition)
Mechanical Engineering
ISBN:
9780134319650
Author:
Russell C. Hibbeler
Publisher:
PEARSON

Thermodynamics: An Engineering Approach
Mechanical Engineering
ISBN:
9781259822674
Author:
Yunus A. Cengel Dr., Michael A. Boles
Publisher:
McGraw-Hill Education

Control Systems Engineering
Mechanical Engineering
ISBN:
9781118170519
Author:
Norman S. Nise
Publisher:
WILEY

Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:
9781337093347
Author:
Barry J. Goodno, James M. Gere
Publisher:
Cengage Learning

Engineering Mechanics: Statics
Mechanical Engineering
ISBN:
9781118807330
Author:
James L. Meriam, L. G. Kraige, J. N. Bolton
Publisher:
WILEY