Find the radius of A Circle in Central angle of yr/3 radians detevmines Sector of area which a 6m?
Find the radius of A Circle in Central angle of yr/3 radians detevmines Sector of area which a 6m?
Trigonometry (11th Edition)
11th Edition
ISBN:9780134217437
Author:Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Chapter1: Trigonometric Functions
Section: Chapter Questions
Problem 1RE:
1. Give the measures of the complement and the supplement of an angle measuring 35°.
Related questions
Question
Need help finding the answer
![### Problem Statement
Find the radius of a circle in which a central angle of \(\frac{4\pi}{3}\) radians determines a sector of area 6 m\(^2\).
### Explanation
This problem involves determining the radius of a circle given the central angle in radians and the area of the sector of the circle.
#### Formula to use:
The area \(A\) of a sector with a central angle \(\theta\) (in radians) and radius \(r\) is given by the formula:
\[ A = \frac{1}{2} r^2 \theta \]
#### Calculation Steps:
1. Plug in the values into the formula:
\[ 6 = \frac{1}{2} r^2 \times \frac{4\pi}{3} \]
2. Simplify and solve for \(r\).
#### Graph/Diagram Description
The image contains a rough sketch of a circle with a labeled sector, demonstrating the relationship between the central angle and the area of the sector. The angle \(\frac{4\pi}{3}\) is illustrated to show the span of the sector in relation to the circle.
By following these steps, we can find the radius of the circle. This problem combines knowledge of geometry and algebra to solve for unknown measurements.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F116eaff4-03e4-4994-8958-7f2150795223%2F52ebb96c-3c72-4774-b9fb-223998a6d909%2F60bso1v_processed.jpeg&w=3840&q=75)
Transcribed Image Text:### Problem Statement
Find the radius of a circle in which a central angle of \(\frac{4\pi}{3}\) radians determines a sector of area 6 m\(^2\).
### Explanation
This problem involves determining the radius of a circle given the central angle in radians and the area of the sector of the circle.
#### Formula to use:
The area \(A\) of a sector with a central angle \(\theta\) (in radians) and radius \(r\) is given by the formula:
\[ A = \frac{1}{2} r^2 \theta \]
#### Calculation Steps:
1. Plug in the values into the formula:
\[ 6 = \frac{1}{2} r^2 \times \frac{4\pi}{3} \]
2. Simplify and solve for \(r\).
#### Graph/Diagram Description
The image contains a rough sketch of a circle with a labeled sector, demonstrating the relationship between the central angle and the area of the sector. The angle \(\frac{4\pi}{3}\) is illustrated to show the span of the sector in relation to the circle.
By following these steps, we can find the radius of the circle. This problem combines knowledge of geometry and algebra to solve for unknown measurements.
Expert Solution
Step 1
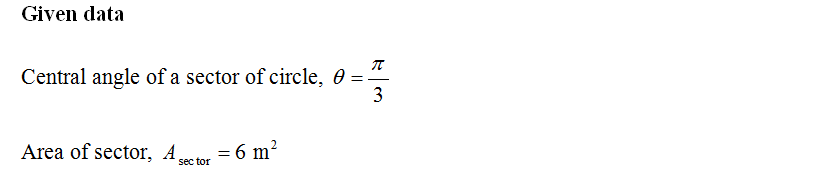
Step by step
Solved in 4 steps with 5 images

Recommended textbooks for you

Trigonometry (11th Edition)
Trigonometry
ISBN:
9780134217437
Author:
Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:
PEARSON

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781305652224
Author:
Charles P. McKeague, Mark D. Turner
Publisher:
Cengage Learning


Trigonometry (11th Edition)
Trigonometry
ISBN:
9780134217437
Author:
Margaret L. Lial, John Hornsby, David I. Schneider, Callie Daniels
Publisher:
PEARSON

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781305652224
Author:
Charles P. McKeague, Mark D. Turner
Publisher:
Cengage Learning


Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781337278461
Author:
Ron Larson
Publisher:
Cengage Learning