Homework Help is Here – Start Your Trial Now!
Math
Algebra
Find the equation of a parabola that will fit these constraints. 2. How wide is the channel with a minimum 60-foot vertical clearance for the parabola in question 1? 3. Find the equation of a semiellipse that will fit these constraints. 4. How wide is the channel with a minimum 60-foot vertical clearance for the semiellipse in question 3? 5. Which of these bridge designs would you choose, and why? 6. Suppose the tallest fishing ship installs a new antenna which raises the center height by 12 feet. How far off of center (to the left or right) can the ship now travel and still pass under the bridge without damage to the antenna a. for the parabola? b. for the semiellipse

Find the equation of a parabola that will fit these constraints. 2. How wide is the channel with a minimum 60-foot vertical clearance for the parabola in question 1? 3. Find the equation of a semiellipse that will fit these constraints. 4. How wide is the channel with a minimum 60-foot vertical clearance for the semiellipse in question 3? 5. Which of these bridge designs would you choose, and why? 6. Suppose the tallest fishing ship installs a new antenna which raises the center height by 12 feet. How far off of center (to the left or right) can the ship now travel and still pass under the bridge without damage to the antenna a. for the parabola? b. for the semiellipse

Elementary Geometry for College Students
Elementary Geometry for College Students
6th Edition
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Daniel C. Alexander, Geralyn M. Koeberlein
Chapter9: Surfaces And Solids
Section9.2: Pyramids, Area, And Volume
Problem 35E
See similar textbooks
icon
Related questions
Question

Find the equation of a parabola that will fit these constraints.
2. How wide is the channel with a minimum 60-foot vertical clearance for the
parabola in question 1?
3. Find the equation of a semiellipse that will fit these constraints.
4. How wide is the channel with a minimum 60-foot vertical clearance for the
semiellipse in question 3?
5. Which of these bridge designs would you choose, and why?
6. Suppose the tallest fishing ship installs a new antenna which raises the center
height by 12 feet. How far off of center (to the left or right) can the ship now
travel and still pass under the bridge without damage to the antenna
a. for the parabola?
b. for the semiellipse

1. Find the equation of a parabola that will fit these constraints. How wide is the channel with a minimum 60-foot vertical clearance for the parabola in question 1? Find the equation of a semiellipse that will fit these constraints. 4. How wide is the channel with a minimum 60-foot vertical clearance for the semiellipse in question 3? Which of these bridge designs would you choose, and why? Suppose the tallest fishing ship installs a new antenna which raises the center height by 12 feet. How far off of center (to the left or right) can the ship now travel and still pass under the bridge without damage to the antenna 2. 3. 5. 6. 60 ft a. for the parabola? b. for the semiellipse? 300 ft
Transcribed Image Text:1. Find the equation of a parabola that will fit these constraints. How wide is the channel with a minimum 60-foot vertical clearance for the parabola in question 1? Find the equation of a semiellipse that will fit these constraints. 4. How wide is the channel with a minimum 60-foot vertical clearance for the semiellipse in question 3? Which of these bridge designs would you choose, and why? Suppose the tallest fishing ship installs a new antenna which raises the center height by 12 feet. How far off of center (to the left or right) can the ship now travel and still pass under the bridge without damage to the antenna 2. 3. 5. 6. 60 ft a. for the parabola? b. for the semiellipse? 300 ft
CHAPTER 8 PROJECT Constructing a Bridge Plans are in process to develop an uninhabited coastal island into a new resort. Before development can begin, a bridge must be constructed joining the island to the mainland. Two possibilities are being considered for the support structure of the bridge. The archway could be built as a parabola, or in the shape of a semiellipse. Assume all measurements that follow refer to dimensions at high tide. The county building inspector has deemed that in order to establish a solid foundation, the space between supports must be at most 300 feet and the height at the center of the arch should be 80 feet. There is a commercial fishing dock located on the mainland whose fishing vessels travel constantly along this intracoastal waterway. The tallest of these ships requires 60 feet of clearance to pass comfortably beneath the bridge. With these restrictions, the width of a channel with a minimum height of 60 feet has to be determined for both possible shapes of the bridge to confirm that it will be suitable for the water traffic beneath it. ? ft 60 ft 80 ft 300 ft
Transcribed Image Text:CHAPTER 8 PROJECT Constructing a Bridge Plans are in process to develop an uninhabited coastal island into a new resort. Before development can begin, a bridge must be constructed joining the island to the mainland. Two possibilities are being considered for the support structure of the bridge. The archway could be built as a parabola, or in the shape of a semiellipse. Assume all measurements that follow refer to dimensions at high tide. The county building inspector has deemed that in order to establish a solid foundation, the space between supports must be at most 300 feet and the height at the center of the arch should be 80 feet. There is a commercial fishing dock located on the mainland whose fishing vessels travel constantly along this intracoastal waterway. The tallest of these ships requires 60 feet of clearance to pass comfortably beneath the bridge. With these restrictions, the width of a channel with a minimum height of 60 feet has to be determined for both possible shapes of the bridge to confirm that it will be suitable for the water traffic beneath it. ? ft 60 ft 80 ft 300 ft
Expert Solution
Step 1: Given information

Note: It is a multipart question. No specific part has been asked.
So, We will solve the first four parts for you. Other parts can be asked as a new query.

 

Given: 

 

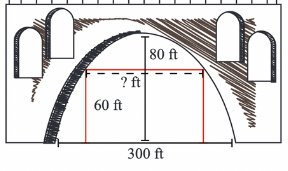
Algebra homework question answer, step 1, image 1

Constraint: 

The maximum height  = 80ft

The maximum width   = 300ft

 

General equation of parabola : 

x2=-4ay-k +h

steps

Step by step

Solved in 5 steps with 6 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Recommended textbooks for you
Elementary Geometry for College Students
Elementary Geometry for College Students
Geometry
ISBN:
9781285195698
Author:
Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:
Cengage Learning
Algebra & Trigonometry with Analytic Geometry
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage
Elementary Geometry For College Students, 7e
Elementary Geometry For College Students, 7e
Geometry
ISBN:
9781337614085
Author:
Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:
Cengage,
College Algebra
College Algebra
Algebra
ISBN:
9781337282291
Author:
Ron Larson
Publisher:
Cengage Learning
Trigonometry (MindTap Course List)
Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781337278461
Author:
Ron Larson
Publisher:
Cengage Learning
Holt Mcdougal Larson Pre-algebra: Student Edition…
Holt Mcdougal Larson Pre-algebra: Student Edition…
Algebra
ISBN:
9780547587776
Author:
HOLT MCDOUGAL
Publisher:
HOLT MCDOUGAL
SEE MORE TEXTBOOKS