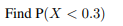Let X have pdf= {(a) Determine the distribution function Fx (x), by firstly finding k.fxkr(1-x), 0≤x≤ 1;otherwise.

Answer: - Given, X has the pdf fx(x) = kx(1 - x)0≤x≤10otherwise Find…

Answered: Let X have pdf fx(x) = { kr(1-2),…

Let X have pdf fx(x) = { kr(1-2), 0≤x≤1; 0, otherwise. (a) Determine the distribution function Fx (2), by firstly finding k.

A First Course in Probability (10th Edition)

10th Edition

ISBN:9780134753119

Author:Sheldon Ross

Publisher:Sheldon Ross

Chapter1: Combinatorial Analysis

Section: Chapter Questions

Problem 1.1P: a. How many different 7-place license plates are possible if the first 2 places are for letters and...

See similar textbooks

Related questions

Q: Let X and Y be independent v.a with uniform distribution on the interval (0, 20) and (0, 30)…

Q: Let X be a Poisson distribution with A as parameter: a. Find E(X) and VAR(X) b. Find the…

A: For the random variable following the Poisson distribution, the variable is assumed to take…

Q: Find the distribution function for f(x). (0.5 1 1<x<2 ƒ(x) = { ½ x x 2<x<3 0 elsewhere

Q: Find the mean value of f(x) = |x| on the interval [-1, 4]. %3D

A: Given that: f(x)=|x| in [-1, 4]

Q: 1. a) Find the mean value u of the function f (x) = |3x| +3 on the interval [-2, 1] . %3!

Q: Find all numbers c which satisfy the conclusion of the Mean Value Theorem for the function f(x) = x…

Q: Let X = U(3) find Var(-x) and distribution function.

A: It is given that the random variable X~U(3) Now, in uniform distribution we have two intervals 'a'…

Q: Let Y be continuous defined on (0, 1) with pdf given by f(y) = 2(1-y), 0 0.67

A: Introduction: Denote the random variable of interest as Y.

Q: Let X has uniform distribution on [-1,1]. Find E(X|X²).

A: Given: X has uniform distribution on [-1,1]. Then the pdf is: f (x)=12for -1<X<10Otherwise

Q: 3. Assume that an insurance company will experience a loss X that is modeled by a uniform…

A: Given,A random varible X~U[2,10]f(x)=110-2f(x)=18 ; 2≤x≤10

Q: Let X be distributed as an exponential with a mean of 1.5. find: a) P(X = 0.16) b) P(X 0.372)

A: Given that Mean=1.5 Mean=1/λ 1.5=1/λ λ=1/1.5 X~exp(λ) NOTE:- According to bartleby guidelines…

Q: What is the pdf of this distribution? (a) 4x - x² (b) 1/7 (2x² - 12/²2) x3 - 9 3 1 1 (c) - (4x − x²)…

Q: Suppose X1, . . . , Xn are i.i.d. from a continuous distribution with p.d.f. fθ(x)=1/2(1+θx)if…

A: X1, . . . , Xn are independent and identically distributed (i.i.d) random variables with pdf…

Q: 3. Let X be a random variable with distribution function P(X ≤x} = { 0 x 1 if x ≤ 0, if 0 1. Let F…

Q: Does a distribution exist for which: Mx(t) = (t)/(t-1) for |t| < 1? If yes, find it, otherwise prove…

A: Given the distribution function, Mx(t) = (t)/(t-1) for t < 1

Q: Let X denote the proportion of allotted time that a randomly selected student spends working on a…

Q: Suppose that the distribution of X is in the form f(x) = Cx4 for x in the interval [−1, 2]. (a)…

A: Since you have posted a question with multiple sub-parts, we will solve first three sub- parts for…

Q: 6. If X is t-distributed, show that X² is F-distributed.

Q: Find the mean and standard deviation for each uniform continuous model U(1, 13) U(70, 200) U(3, 92)

A: Obtain the mean and standard deviation for the uniform continuous model U(1,13). Obtain the mean of…

Q: nstants аnd 9. Fx (x) = [1 – a. e-x/b]u (x) is a valid distribution funetion. u (x) is an unit step…

A: Answer: For the given data

Q: Suppose that the conditional distribution of Y given X = x is Poisson with mean E(Y|x) = x, and that…

A: d) From the given information, The conditional distribution of Y given X=x is Poisson distribution…

Q: Consider the joint PDF f(x,y)=4xy for 0<x<1 and 0<y<1. (a) Are X and Y independent? (b) Find both…

A: We have given thatjoint PDF f(x,y)=4xy for 0<x<1 and 0<y<1.

Q: The mean function will be O Bo + B₁X + e O Non of the other answers O E(YX) Bo + B₁ X = O E(Y|X) =…

A: It is given as the simple linear regression model Y = β0 + β1X + e, e ~iid N( 0, σ2 ), i = 1, 2, .…

Q: Let X ∼ Uniform (0, 2). Consider a square with sidelength X. (a) Express the area A as function of…

A: Since you have posted a question with multiple subparts, we will solve the first three complete…

Q: Let X denote the proportion of allotted time that a randomly selected student spends working on a…

A: The pdf of x f(x)=(θ+1)xθ 0<x<1We have to finda... Method of moment estimator of theta b..…

Q: In this question you are required to examine distribution at X(0) and x(1/8fo) x(0) ∈{0,-1 ,1}…

A: Given information: The distributions of X(0) and X(1/8fo) are given.

Q: Let X denote the mean of a random sample of size 25 from the distribution whose pdf is f(x) = x²…

A: We have given that the X-bar denote the mean of a random sample of size 25 from the distribution…

Q: Let X have a uniform distribution on the interval (0, 2). Given X = x, let Y have a (conditional)…

A: (a) The conditional pdf of Y given X = x is a uniform distribution on the interval (0, 0.5x), so:…

Q: (a) Find the inverse function' of the CDF of Exponential(1). (b) Find CDF of X = - log(U). (c) Find…

Q: x >1 f(x) =x10 xs1 ermine the value of k for which f(x) is a legitimate pdf. ain the cumulative…

A: Since the question has multiple sub parts we will solve the first part only. Please resend the…

Q: Calculate the conditional expectation of Y when X E(YX2)

A: The objective is to calculate the conditional expectation of Y when X = 2.

Q: Pind the values of the constants a' and 'b' such that the CDF Кx (х) %3D 1- а.е xb] и (х) is a valid…

Q: Find the Maximum Likelihood Estimator (MLE) of θ.

A: To determine the MLE we have to find the likelihood and log-likelihood functions.

Q: Let X(1) 0. a) Show that X4) and X(6) – X() are independent for any s>r. b) Find the distribution of…

Question

Let X have pdf
= {
(a) Determine the distribution function Fx (x), by firstly finding k.
fx
kr(1-x), 0≤x≤ 1;
otherwise.

Expert Solution

This question has been solved!

Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.

SEE SOLUTION Check out a sample Q&A here

Step 1

VIEW

Step 2

VIEW

Step by step

Solved in 2 steps

SEE SOLUTION Check out a sample Q&A here

Follow-up Questions

Read through expert solutions to related follow-up questions below.

Follow-up Question

(b) Use R to plot the pdf and df of X on the same graph.

Solution

by Bartleby Expert

SEE SOLUTION

Follow-up Question

Solution

by Bartleby Expert

SEE SOLUTION

Similar questions

A) | kx 0 1 B) Obtain the 25th percentile and the 75th percentile of the distribution.
If the function satisfies the mean value theorem for f(x)= x² +3x +5 in [0,1], then f(a)= Choose... The value of 'c' is Choose... f(b)= Choose...
6. Use the moment-generating function of gamma distribution to show that E(X)=a0 and Var (X)=a0²
Let f(x,0) = ex-1 0
If X and Y are two independent uniform distribution with X(0 ,4) and Y(0,6). Find the joint pdf f (x.y). Find P(2.5<X<3.5,1<Y<4)
Consider X and Y are joint distributed with PDFf(x,y)=x+y, 0≤x≤1, 0≤y≤1. (d) Find the marginal distributions of X and Y .(e) Find the conditional distribution of X given Y = y.
Let random sample of n observations from each of the distributions: a. Poisson distribution with parameter θ. b. f(x, θ) = (1/ θ) e-x/θ , 0 < x. In each case find the Minimum Variance Estimator of θ and prove its efficiency.
The random variable U has the following distribution: U 123 PU(u) 0.20 0.40 0.40 (c) Write down the moment generating function (mgf) of U. (d) Use the mgf to help determine var[U].
Assume that X1, X2, X3 ∼ Exp (λ) are independent and evenly distributed with the distribution Exp (λ = 1). (a) Determine the distribution of Y = X1 + X2 + X3 and state its PDF f (y). (b) Determine the distribution of U = 2Y
Let X be a point randomly selected from the unit interval [0, 1]. Consider the random variable Y = (1-X)-¹/2 (a) Sketch Y as a function of X. (b) Find and plot the cdf of Y. (c) Derive the pdf of Y. (d) Compute the following probabilities: P(Y > 1), P(3 < Y < 6), P(Y ≤ 10).