Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
Related questions
Question
![To solve the integral \( \int_{0}^{5} f(x) \, dx \) where
\[
f(x) =
\begin{cases}
3 & \text{for } x < 3 \\
x & \text{for } x \geq 3
\end{cases}
\]
we need to evaluate the integral by considering the piecewise definition of \( f(x) \).
### Steps to Solve:
1. **Break the Integral at the Point of Discontinuity:**
The function \( f(x) \) changes its definition at \( x = 3 \). Thus, we split the integral into two parts:
\[
\int_{0}^{5} f(x) \, dx = \int_{0}^{3} 3 \, dx + \int_{3}^{5} x \, dx
\]
2. **Evaluate Each Integral Separately:**
- For the first integral \( \int_{0}^{3} 3 \, dx \):
- Treating 3 as a constant, the integral is:
\[
\int_{0}^{3} 3 \, dx = 3x \Big|_{0}^{3} = 3(3) - 3(0) = 9
\]
- For the second integral \( \int_{3}^{5} x \, dx \):
- The integral of \( x \) is:
\[
\int_{3}^{5} x \, dx = \frac{x^2}{2} \Big|_{3}^{5} = \left(\frac{5^2}{2} - \frac{3^2}{2}\right) = \left(\frac{25}{2} - \frac{9}{2}\right) = \frac{16}{2} = 8
\]
3. **Add the Results Together:**
Combining the results of the two integrals gives
\[
\int_{0}^{5} f(x) \, dx = 9 + 8 = 17
\]
Thus, the integral of the function from 0 to 5 is 17.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fc58706f5-86d4-4e1b-ad89-6180f41ce69b%2Ffb30be68-4269-4e39-8c1b-943a12bf7021%2Fggbh4w_processed.png&w=3840&q=75)
Transcribed Image Text:To solve the integral \( \int_{0}^{5} f(x) \, dx \) where
\[
f(x) =
\begin{cases}
3 & \text{for } x < 3 \\
x & \text{for } x \geq 3
\end{cases}
\]
we need to evaluate the integral by considering the piecewise definition of \( f(x) \).
### Steps to Solve:
1. **Break the Integral at the Point of Discontinuity:**
The function \( f(x) \) changes its definition at \( x = 3 \). Thus, we split the integral into two parts:
\[
\int_{0}^{5} f(x) \, dx = \int_{0}^{3} 3 \, dx + \int_{3}^{5} x \, dx
\]
2. **Evaluate Each Integral Separately:**
- For the first integral \( \int_{0}^{3} 3 \, dx \):
- Treating 3 as a constant, the integral is:
\[
\int_{0}^{3} 3 \, dx = 3x \Big|_{0}^{3} = 3(3) - 3(0) = 9
\]
- For the second integral \( \int_{3}^{5} x \, dx \):
- The integral of \( x \) is:
\[
\int_{3}^{5} x \, dx = \frac{x^2}{2} \Big|_{3}^{5} = \left(\frac{5^2}{2} - \frac{3^2}{2}\right) = \left(\frac{25}{2} - \frac{9}{2}\right) = \frac{16}{2} = 8
\]
3. **Add the Results Together:**
Combining the results of the two integrals gives
\[
\int_{0}^{5} f(x) \, dx = 9 + 8 = 17
\]
Thus, the integral of the function from 0 to 5 is 17.
Expert Solution
Step 1
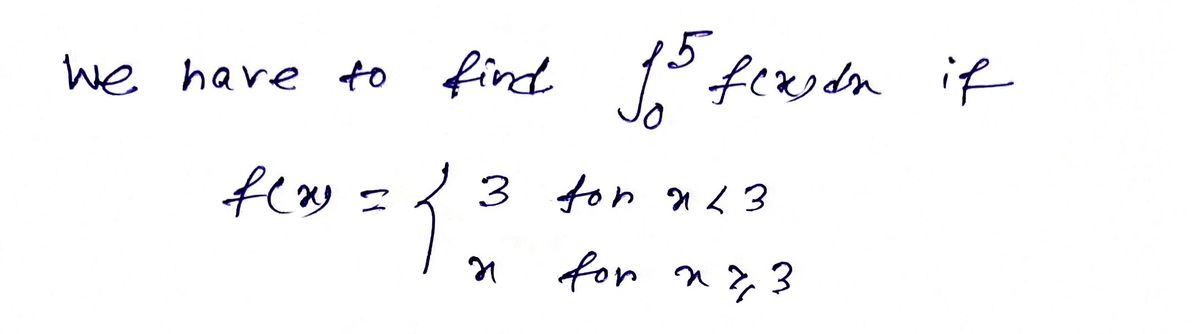
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning