find curves y = y ( x ) such that every point ( x 0 , y 0 ) on the curve divides the tangent line segment at ( x 0 , y 0 ) with endpoints on the coordinate axes into two segments with ratio k : 1 − k, ( 0 < k < 1 ).

step:- 1

Section Formula:- Let SQ be a line segment with end points S $(a_1,b_1) and$Q $(a_2,b_2)$ then let a point P (a,b) on SQ divides SQ in two segment in the ratio $m_1, m_2$ then the co-ordinates of P is

  $a=\frac{m_1{a}_2+m_2{a}_1}{m_1+m_2}, b=\frac{m_1{b}_2+m_2{b}_1}{m_1+m_2}$

Step:- 2

Now, given that a curve y(x) such that every point on curve divides tangent line segment on that point. Then

Let P $(x_0,y_0)$ be a point on curve and SQ be a tangent line segment at P.

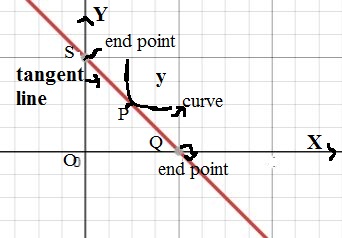
Now, let distance of Q from origin is q than co-ordinates of Q is (q, 0)   [as it lies on x-axis so y=0]

let distance of S from origin is s than co-ordinates of S is (0, s)   [as it lies on Y-axis so x=0]

Step:- 3

Also, given that P divides tangent line segment in two segment with ratio $\frac{k}{(1-k)}$ that is, PS = k and PQ= (1-k).

Here, P divides line SQ internally, than applying Section formula (given above) we get

$$\begin{gathered} x_0=\frac{k q+(1-k) \times 0}{k+(1-k)}, y_0=\frac{k \times 0+(1-k) \times s}{k+(1-k)} \\ {x}_0=\frac{kq}{1}, y_0=\frac{(1-k)s}{1} \\ q=\frac{x_0}{k}, ---\left(1\right) \\ s=\frac{y_0}{(1-k)}---\left(2\right) \end{gathered}$$