Exercises 8. T:R² → R² defined by T(x1,x2) = (ı+x2, x1 – x2 – 1). 9. T:R? → R° defined by T(x1,x2) = (1, x1+ x2, 2.x2) 1. Compute ax + by for each of the following: (а) а %— 2, b %3D —-3, г %3 (2, 4) and y 3 (3, —1). (b) а %3D 10, b %3 -2, х %3 (1,0, —1) and y 3D (2, -4, 3). (c) a = 5, b = -1, x = (4, 2, –1, 1) and y = (-1,3,5, 7). 10. Determine which of the following maps are linear maps. If the map is linear give the matrix associated to the linear map. Explain your reasoning. (») Lı : R* -→ R° where La;)-(****) x + y +3 2y +1 2. Let x = (4, 7) and y = (2, –1). Write the vector ax + By sin x R' where L2 x + y 2y as a vector in coordinates. (b) L2 :R² (c) L3 : R? → R where L3 = x + y 3. Let x = (1, 2), y = (1, –3), and z = (-2, – 1). Show that you can write z = ax + By for some a, BER. 11. Find the 2 x 3 matrix A that satisfies Hint: Set up a system of two linear equations in the un- knowns a and B, and then solve this linear system. (;). (:) Aej = 3 Ae2 = and Aez = 4. Can the vector z = (2, 3, –1) be written as 12. The cross product of two 3-vectors x = y = (y1, Y2, Y3) is the 3-vector (x1, x2, x3) and z = ax + By where x = (2, 3, 0) and y = (1, –1, 1)? x x y = (x2y3 – x3y2, –(x1y3 – x3y1), x1y2 – x2y1). Let K = (2,1, –1). 5. Let x = (3, –2), y = (2, 3), and z = (1,4). For which real numbers a, B, y does (a) Show that the mapping L : R → R defined by ах + Ву + yz%3 (1,—2)? L(x) = x x K is a linear mapping. In Exercises 6 – 9 determine whether the given transformation is linear. (b) Find the 3 x 3 matrix A such that L(x) = Ax, 6. T: R* → R² defined by T(x1,x2, x3) = (x1+2x2-x3, X1- 4.x3). that is, L = LA. 7. T: R² → R² defined by T(x1, x2) = (x1 +x1x2, 2x2). 61
Exercises 8. T:R² → R² defined by T(x1,x2) = (ı+x2, x1 – x2 – 1). 9. T:R? → R° defined by T(x1,x2) = (1, x1+ x2, 2.x2) 1. Compute ax + by for each of the following: (а) а %— 2, b %3D —-3, г %3 (2, 4) and y 3 (3, —1). (b) а %3D 10, b %3 -2, х %3 (1,0, —1) and y 3D (2, -4, 3). (c) a = 5, b = -1, x = (4, 2, –1, 1) and y = (-1,3,5, 7). 10. Determine which of the following maps are linear maps. If the map is linear give the matrix associated to the linear map. Explain your reasoning. (») Lı : R* -→ R° where La;)-(****) x + y +3 2y +1 2. Let x = (4, 7) and y = (2, –1). Write the vector ax + By sin x R' where L2 x + y 2y as a vector in coordinates. (b) L2 :R² (c) L3 : R? → R where L3 = x + y 3. Let x = (1, 2), y = (1, –3), and z = (-2, – 1). Show that you can write z = ax + By for some a, BER. 11. Find the 2 x 3 matrix A that satisfies Hint: Set up a system of two linear equations in the un- knowns a and B, and then solve this linear system. (;). (:) Aej = 3 Ae2 = and Aez = 4. Can the vector z = (2, 3, –1) be written as 12. The cross product of two 3-vectors x = y = (y1, Y2, Y3) is the 3-vector (x1, x2, x3) and z = ax + By where x = (2, 3, 0) and y = (1, –1, 1)? x x y = (x2y3 – x3y2, –(x1y3 – x3y1), x1y2 – x2y1). Let K = (2,1, –1). 5. Let x = (3, –2), y = (2, 3), and z = (1,4). For which real numbers a, B, y does (a) Show that the mapping L : R → R defined by ах + Ву + yz%3 (1,—2)? L(x) = x x K is a linear mapping. In Exercises 6 – 9 determine whether the given transformation is linear. (b) Find the 3 x 3 matrix A such that L(x) = Ax, 6. T: R* → R² defined by T(x1,x2, x3) = (x1+2x2-x3, X1- 4.x3). that is, L = LA. 7. T: R² → R² defined by T(x1, x2) = (x1 +x1x2, 2x2). 61
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Topic Video
Question
Only for highlighted questions please!

Transcribed Image Text:Exercises
8. T: R? → R² defined by T (x1,x2) = (x1+x2, x1 – X2 – 1).
9. T: R² → R³ defined by T(x1,x2) = (1, x1+x2,2x2)
1. Compute ax + by for each of the following:
10. Determine which of the following maps are linear maps.
= (3, –1).
= (2, –4, 3).
(c) a = 5, b = –1, x = (4, 2, – 1, 1) and y = (-1, 3, 5, 7).
(а) а — 2, b — -3, х —
(2, 4) and y =
If the map is linear give the matrix associated to the linear
(b) а — 10, b 3 — 2, х — (1,0, —1) and y —
map. Explain your reasoning.
;)-(+1
x + y + 3
2y + 1
(a) L1 : R? → R² where L1 (
2. Let x =
(4, 7) and y = (2, –1). Write the vector ax + By
sin x
as a vector in coordinates.
(b) L2 : R² –→ R° where L2
x + Y
2y
(;)
3. Let x =
(1, 2), y = (1, –-3), and z = (-2, – 1). Show that
(c) L3 : R² –→ R where L3
= x + y
you can write
z = ax + By
for some a, ß E R.
11. Find the 2 x 3 matrix A that satisfies
Hint: Set up a system of two linear equations in the un-
knowns a and B, and then solve this linear system.
(:).
2
Aei =
Ae2
and
Аез
3
-1
4. Can the vector z =
(2, 3, – 1) be written as
12. The cross product of two 3-vectors x =
(x1, 12, x3) and
z = ax + By
y = (y1, Y2, Y3) is the 3-vector
where x =
(2, 3,0) and y = (1, –1, 1)?
тху3 (х2уз — г:3у2, — (х1уз — «зу1), х192 — 22у1).
Let K = (2,1, -1).
: (3, —2), у — (2, 3), and z %3D
B,y does
5. Let x =
(1,4). For which real
(a) Show that the mapping L : R³ → R³ defined by
numbers a,
ат + By + 72 3 (1,—2)?
L(x) = x x K
is a linear mapping.
In Exercises 6 – 9 determine whether the given transformation
is linear.
(b) Find the 3 × 3 matrix A such that
L(x) = Ax,
6. T: R* → R² defined by T(x1, x2, x3) = (xı+2x2-x3,X1¬-
4x3).
that is, L = LẠ.
7. T: R² → R² defined by T(x1,x2) = (x1 +x1£2,2x2).
61
Expert Solution
Step 1
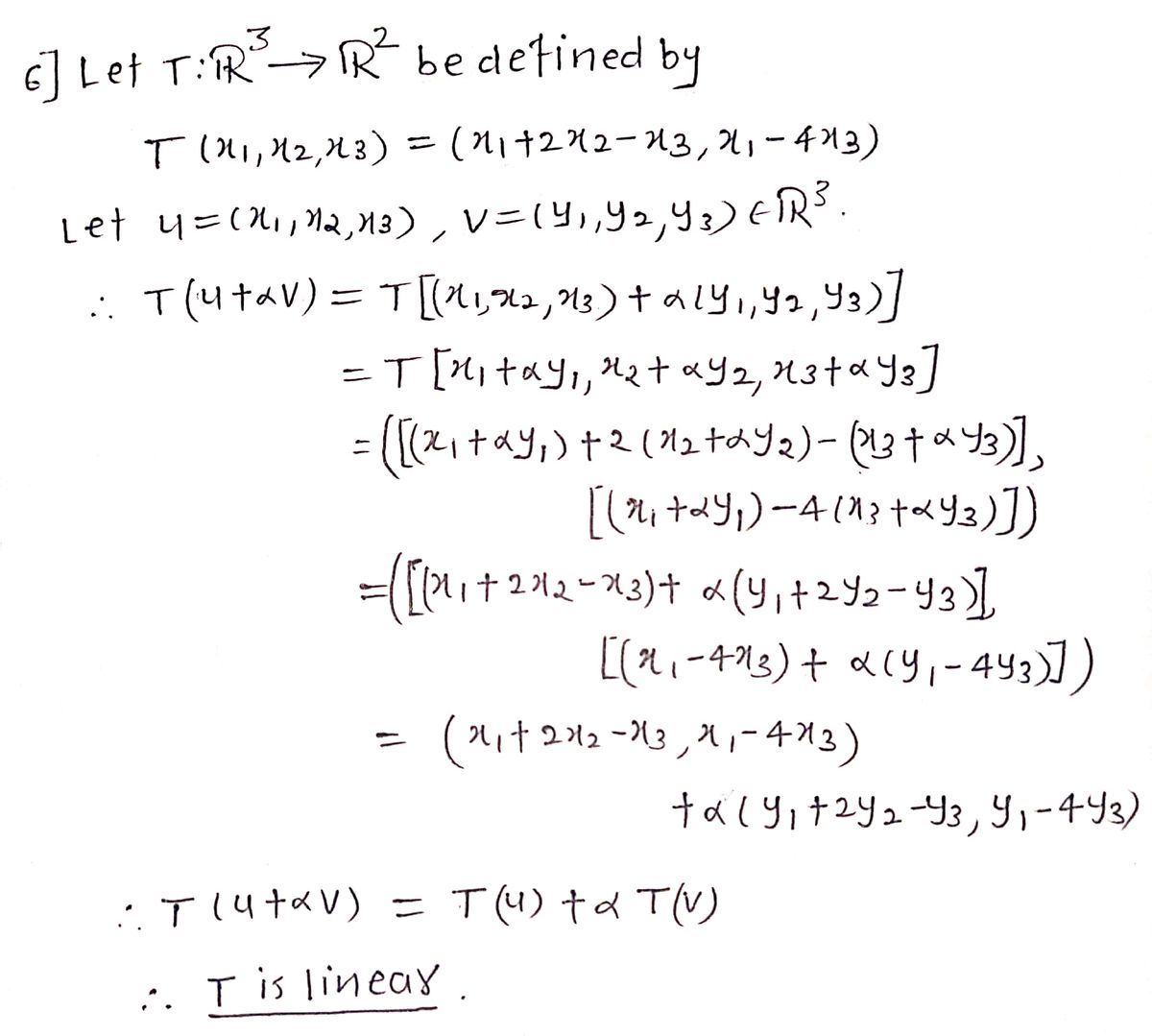
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

