Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
Related questions
Question
100%
I'm not sure what I'm doing wrong. I have attached the assignment and the work I've done.
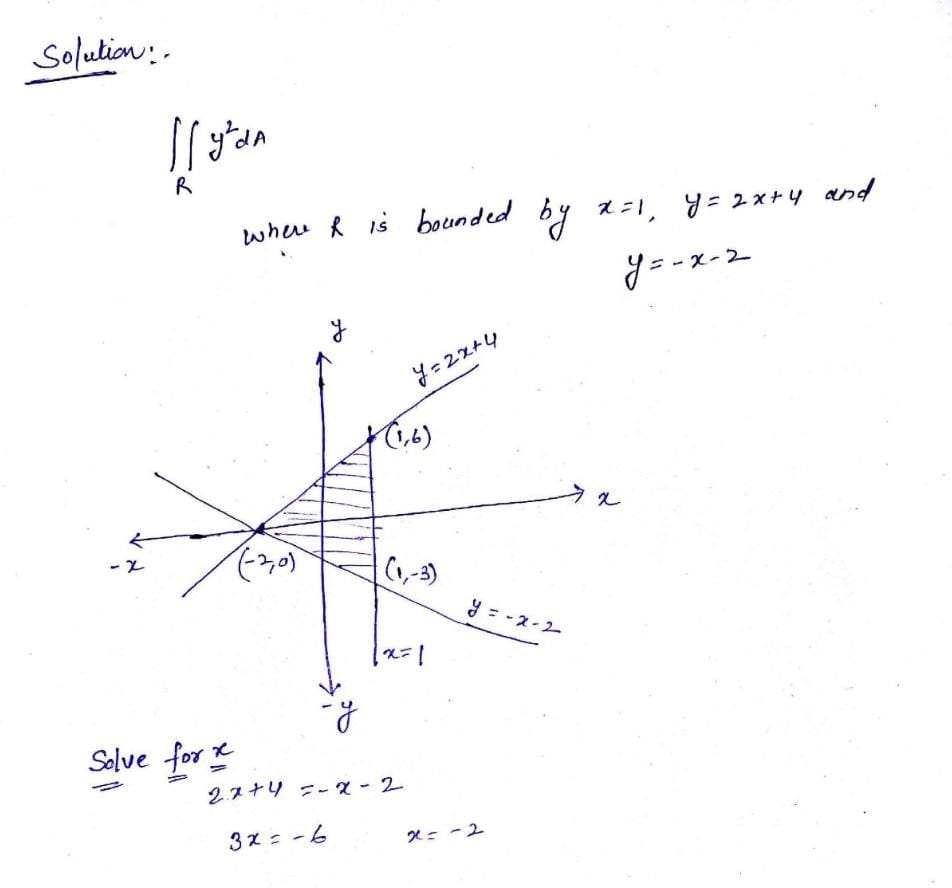
![**Problem Statement:**
Evaluate the following integral, where \( R \) is bounded by \( x = 1 \), \( y = 2x + 4 \), and \( y = -x - 2 \).
\[
\iint_R y^2 \, dA
\]
**Boundary Conditions Explanation:**
The region \( R \) is defined by the intersection of three lines in the Cartesian plane:
- The vertical line \( x = 1 \)
- The line \( y = 2x + 4 \), which is a straight line with a slope of 2 and a y-intercept at +4
- The line \( y = -x - 2 \), which is a straight line with a slope of -1 and a y-intercept at -2
These lines form a bounded region \( R \), and the integral specifies the need to evaluate the function \( y^2 \) over this area.
**Graphical Representation:**
The enclosed region can be visualized by plotting these lines:
1. **\( x = 1 \)**: A vertical line crossing the x-axis at 1.
2. **\( y = 2x + 4 \)**: This line slants upwards, intersecting the y-axis at +4.
3. **\( y = -x - 2 \)**: This line slants downwards, intersecting the y-axis at -2.
The region \( R \) is where these lines intersect each other, forming a closed area on the graph over which the double integral is evaluated to find the total contribution of \( y^2 \) within this boundary.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F48ae96ba-8296-4f48-84d9-a65ba8f4727e%2F614a1d33-74d8-4edb-b362-827dc59a86c8%2Ffen2e7e_processed.png&w=3840&q=75)
Transcribed Image Text:**Problem Statement:**
Evaluate the following integral, where \( R \) is bounded by \( x = 1 \), \( y = 2x + 4 \), and \( y = -x - 2 \).
\[
\iint_R y^2 \, dA
\]
**Boundary Conditions Explanation:**
The region \( R \) is defined by the intersection of three lines in the Cartesian plane:
- The vertical line \( x = 1 \)
- The line \( y = 2x + 4 \), which is a straight line with a slope of 2 and a y-intercept at +4
- The line \( y = -x - 2 \), which is a straight line with a slope of -1 and a y-intercept at -2
These lines form a bounded region \( R \), and the integral specifies the need to evaluate the function \( y^2 \) over this area.
**Graphical Representation:**
The enclosed region can be visualized by plotting these lines:
1. **\( x = 1 \)**: A vertical line crossing the x-axis at 1.
2. **\( y = 2x + 4 \)**: This line slants upwards, intersecting the y-axis at +4.
3. **\( y = -x - 2 \)**: This line slants downwards, intersecting the y-axis at -2.
The region \( R \) is where these lines intersect each other, forming a closed area on the graph over which the double integral is evaluated to find the total contribution of \( y^2 \) within this boundary.
![Certainly! Here is a transcription of the text found in the image, formatted as if for an educational website:
---
## Double Integral Calculation
**Problem**
Evaluate the double integral \(\int \int_R y^3 \, dA\), where \(x = 1, y = 2x+4, y = -x-2\).
**Given Region**
- \(-2 \leq x \leq 1\)
- \(-2 \leq y \leq 2x+4\)
**Step-by-Step Solution**
1. **Set Up Integral:**
\[
\int_{-2}^{1} \left( \int_{-x-2}^{2x+4} y^2 \, dy \right) \, dx
\]
2. **Integrate with respect to \(y\):**
\[
= \int_{-2}^{1} \frac{y^3}{3} \bigg|_{-x-2}^{2x+4} \, dx
\]
3. **Evaluate the inner integral:**
\[
= \int_{-2}^{1} \left[ \frac{(2x+4)^3}{3} - \frac{(-x-2)^3}{3} \right] \, dx
\]
4. **Substitute and Simplify:**
\[
= \int_{-2}^{1} \frac{1}{3} \left[ 22(x+2)^3 - (-1)(x+1)^3 \right] \, dx
\]
5. **Change of Variables:**
Let \(u = x+3\), \(du = dx\).
6. **New Integral Bounds:**
\[
= \int_{1}^{4} \frac{9}{3}(x+3)^3 \, dx
\]
7. **Integration with respect to \(x\):**
\[
= \frac{9}{3} \left[ \frac{(x+3)^4}{4} \right]_1^4
\]
8. **Calculate the Definite Integral:**
\[
= \frac{9}{3} \left[ \frac{64}{4} - \frac{1}{4} \](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F48ae96ba-8296-4f48-84d9-a65ba8f4727e%2F614a1d33-74d8-4edb-b362-827dc59a86c8%2Foof2tk3_processed.jpeg&w=3840&q=75)
Transcribed Image Text:Certainly! Here is a transcription of the text found in the image, formatted as if for an educational website:
---
## Double Integral Calculation
**Problem**
Evaluate the double integral \(\int \int_R y^3 \, dA\), where \(x = 1, y = 2x+4, y = -x-2\).
**Given Region**
- \(-2 \leq x \leq 1\)
- \(-2 \leq y \leq 2x+4\)
**Step-by-Step Solution**
1. **Set Up Integral:**
\[
\int_{-2}^{1} \left( \int_{-x-2}^{2x+4} y^2 \, dy \right) \, dx
\]
2. **Integrate with respect to \(y\):**
\[
= \int_{-2}^{1} \frac{y^3}{3} \bigg|_{-x-2}^{2x+4} \, dx
\]
3. **Evaluate the inner integral:**
\[
= \int_{-2}^{1} \left[ \frac{(2x+4)^3}{3} - \frac{(-x-2)^3}{3} \right] \, dx
\]
4. **Substitute and Simplify:**
\[
= \int_{-2}^{1} \frac{1}{3} \left[ 22(x+2)^3 - (-1)(x+1)^3 \right] \, dx
\]
5. **Change of Variables:**
Let \(u = x+3\), \(du = dx\).
6. **New Integral Bounds:**
\[
= \int_{1}^{4} \frac{9}{3}(x+3)^3 \, dx
\]
7. **Integration with respect to \(x\):**
\[
= \frac{9}{3} \left[ \frac{(x+3)^4}{4} \right]_1^4
\]
8. **Calculate the Definite Integral:**
\[
= \frac{9}{3} \left[ \frac{64}{4} - \frac{1}{4} \
Expert Solution
Step 1
Step by step
Solved in 4 steps with 4 images

Recommended textbooks for you

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning