Homework Help is Here – Start Your Trial Now!
Engineering
Electrical Engineering
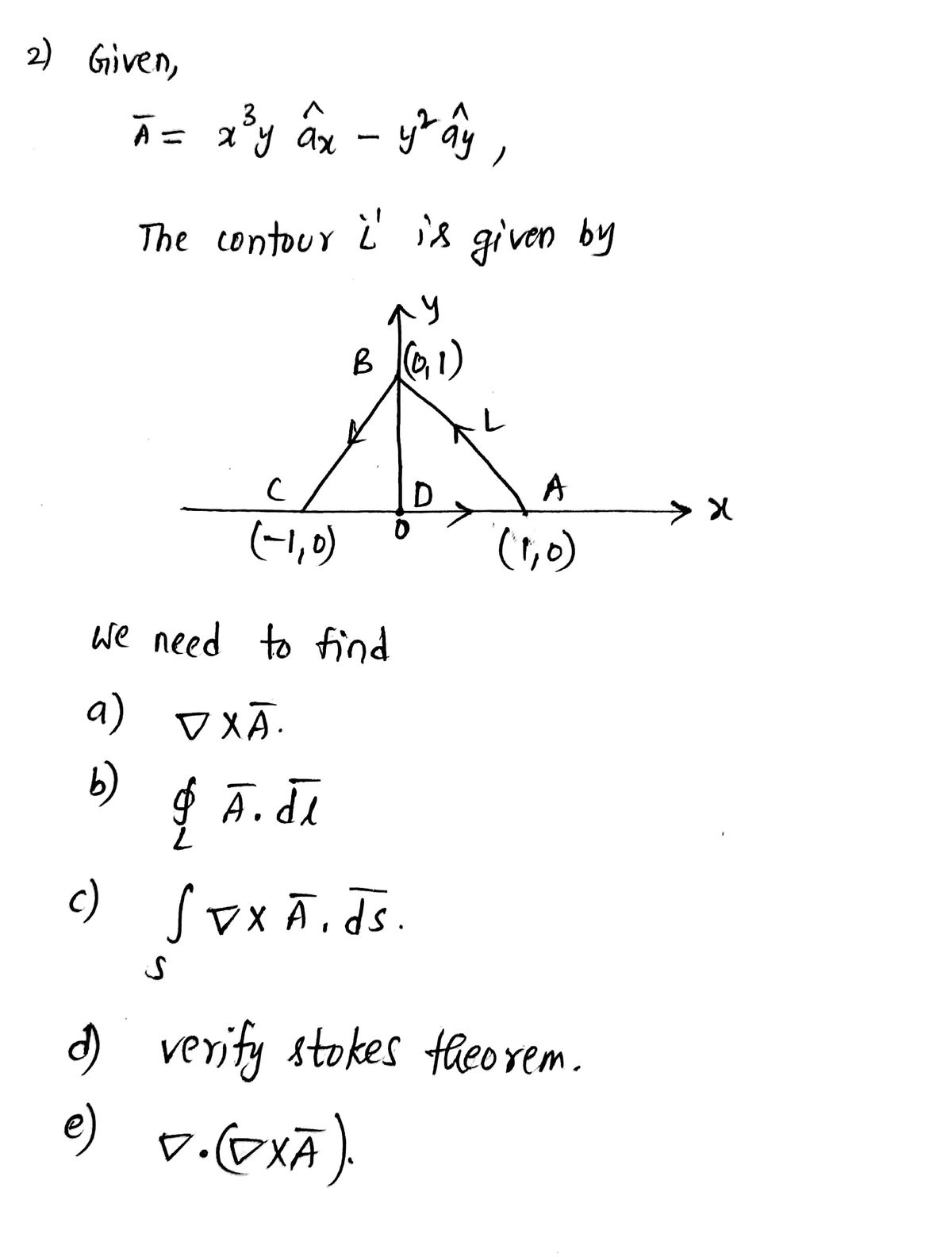
**Problem 2:** Let \(\vec{A} = x^3y \, \hat{a}_x - y^2 \, \hat{a}_y\), and let \(L\) be a contour as shown. a. Find \(\nabla \times \vec{A}\). b. Find \(\oint_L \vec{A} \cdot d\vec{l}\). c. Find \(\iint_S \nabla \times \vec{A} \cdot d\vec{S}\) where \(S\) is the area bounded by \(L\). d. Show that Stokes's Theorem is satisfied. e. Find \(\nabla \cdot (\nabla \times \vec{A})\). **Diagram Explanation:** The diagram is a triangular representation in the xy-plane. It shows a triangular area with vertices at \((0,0)\), \((1,0)\), and \((0,1)\). The arrows indicate that the contour \(L\) follows the edges of the triangle. The arrow directions suggest an anti-clockwise traversal around the triangle's vertices. The area \(S\) mentioned in the problem is the area enclosed within this triangular contour.

**Problem 2:** Let \(\vec{A} = x^3y \, \hat{a}_x - y^2 \, \hat{a}_y\), and let \(L\) be a contour as shown. a. Find \(\nabla \times \vec{A}\). b. Find \(\oint_L \vec{A} \cdot d\vec{l}\). c. Find \(\iint_S \nabla \times \vec{A} \cdot d\vec{S}\) where \(S\) is the area bounded by \(L\). d. Show that Stokes's Theorem is satisfied. e. Find \(\nabla \cdot (\nabla \times \vec{A})\). **Diagram Explanation:** The diagram is a triangular representation in the xy-plane. It shows a triangular area with vertices at \((0,0)\), \((1,0)\), and \((0,1)\). The arrows indicate that the contour \(L\) follows the edges of the triangle. The arrow directions suggest an anti-clockwise traversal around the triangle's vertices. The area \(S\) mentioned in the problem is the area enclosed within this triangular contour.

Introductory Circuit Analysis (13th Edition)
Introductory Circuit Analysis (13th Edition)
13th Edition
ISBN:9780133923605
Author:Robert L. Boylestad
Publisher:Robert L. Boylestad
Chapter1: Introduction
Section: Chapter Questions
Problem 1P: Visit your local library (at school or home) and describe the extent to which it provides literature...
See similar textbooks
icon
Related questions
Question

2

**Problem 2:** Let \(\vec{A} = x^3y \, \hat{a}_x - y^2 \, \hat{a}_y\), and let \(L\) be a contour as shown. a. Find \(\nabla \times \vec{A}\). b. Find \(\oint_L \vec{A} \cdot d\vec{l}\). c. Find \(\iint_S \nabla \times \vec{A} \cdot d\vec{S}\) where \(S\) is the area bounded by \(L\). d. Show that Stokes's Theorem is satisfied. e. Find \(\nabla \cdot (\nabla \times \vec{A})\). **Diagram Explanation:** The diagram is a triangular representation in the xy-plane. It shows a triangular area with vertices at \((0,0)\), \((1,0)\), and \((0,1)\). The arrows indicate that the contour \(L\) follows the edges of the triangle. The arrow directions suggest an anti-clockwise traversal around the triangle's vertices. The area \(S\) mentioned in the problem is the area enclosed within this triangular contour.
Transcribed Image Text:**Problem 2:** Let \(\vec{A} = x^3y \, \hat{a}_x - y^2 \, \hat{a}_y\), and let \(L\) be a contour as shown. a. Find \(\nabla \times \vec{A}\). b. Find \(\oint_L \vec{A} \cdot d\vec{l}\). c. Find \(\iint_S \nabla \times \vec{A} \cdot d\vec{S}\) where \(S\) is the area bounded by \(L\). d. Show that Stokes's Theorem is satisfied. e. Find \(\nabla \cdot (\nabla \times \vec{A})\). **Diagram Explanation:** The diagram is a triangular representation in the xy-plane. It shows a triangular area with vertices at \((0,0)\), \((1,0)\), and \((0,1)\). The arrows indicate that the contour \(L\) follows the edges of the triangle. The arrow directions suggest an anti-clockwise traversal around the triangle's vertices. The area \(S\) mentioned in the problem is the area enclosed within this triangular contour.
Expert Solution
Step 1: State the given data.

Electrical Engineering homework question answer, step 1, image 1

steps

Step by step

Solved in 7 steps with 10 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Similar questions
Recommended textbooks for you
Introductory Circuit Analysis (13th Edition)
Introductory Circuit Analysis (13th Edition)
Electrical Engineering
ISBN:
9780133923605
Author:
Robert L. Boylestad
Publisher:
PEARSON
Delmar's Standard Textbook Of Electricity
Delmar's Standard Textbook Of Electricity
Electrical Engineering
ISBN:
9781337900348
Author:
Stephen L. Herman
Publisher:
Cengage Learning
Programmable Logic Controllers
Programmable Logic Controllers
Electrical Engineering
ISBN:
9780073373843
Author:
Frank D. Petruzella
Publisher:
McGraw-Hill Education
Fundamentals of Electric Circuits
Fundamentals of Electric Circuits
Electrical Engineering
ISBN:
9780078028229
Author:
Charles K Alexander, Matthew Sadiku
Publisher:
McGraw-Hill Education
Electric Circuits. (11th Edition)
Electric Circuits. (11th Edition)
Electrical Engineering
ISBN:
9780134746968
Author:
James W. Nilsson, Susan Riedel
Publisher:
PEARSON
Engineering Electromagnetics
Engineering Electromagnetics
Electrical Engineering
ISBN:
9780078028151
Author:
Hayt, William H. (william Hart), Jr, BUCK, John A.
Publisher:
Mcgraw-hill Education,
SEE MORE TEXTBOOKS