ecade-old study found that the proportion, p , of high school seniors who believed that "getting rich" was an important personal goal was 80%. A researcher decides to test whether or not that percentage still stands. He finds that, among the 220 high school seniors in his random sample, 178 believe that "getting rich" is an important goal. Can he conclude, at the 0.05 level of significance, that the proportion has indeed changed? Perform a two-tailed test. Then complete the parts below.
A decade-old study found that the proportion, p , of high school seniors who believed that "getting rich" was an important personal goal was 80%. A researcher decides to test whether or not that percentage still stands. He finds that, among the 220 high school seniors in his random sample, 178 believe that "getting rich" is an important goal. Can he conclude, at the
Perform a two-tailed test. Then complete the parts below.
Carry your intermediate computations to three or more decimal places and round your answers as specified in the table. (If necessary, consult a list of formulas.)
| (a) | State the null hypothesis
H0?
H1?
|
|
|
H0:?
|
||
|
H1:?
|
||
| (b) | Determine the type of test statistic to use. | |
| ▼(Choose one) chi square ? z.? t ? f ? |
|
|
| (c) | Find the value of the test statistic. (Round to three or more decimal places.) | |
|
|
||
| (d) | Find the two critical values. ?(Round to three or more decimal places.) | |
|
and
|
||
| (e) |
Can we conclude that the proportion of high school seniors who believe that "getting rich" is an important goal has changed? yes or no ? |
|
The following null and alternative hypotheses need to be tested:
This corresponds to a two-tailed test.
A z-test for one population proportion needs to be used.
Based on the information provided, the significance level is , and the critical value for a two-tailed test is . (from the standard normal table).
The z-statistic is computed as follows:
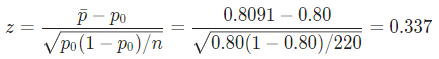
Since it is observed that , it is then concluded that the null hypothesis is not rejected.
Therefore, there is not enough evidence to claim that the population proportion is different than 80%, at the significance level.
Step by step
Solved in 2 steps with 1 images









