(e) Explain why you might want to potentially use the formula n > 4h? instead of n 2 2P (1 – p) when calculating the sample size required when finding a confidence interval h2 for the population proportion. In the formula, h represents the amount of error you are willing to accept, and p represents the sample proportion.
(e) Explain why you might want to potentially use the formula n > 4h? instead of n 2 2P (1 – p) when calculating the sample size required when finding a confidence interval h2 for the population proportion. In the formula, h represents the amount of error you are willing to accept, and p represents the sample proportion.
MATLAB: An Introduction with Applications
6th Edition
ISBN:9781119256830
Author:Amos Gilat
Publisher:Amos Gilat
Chapter1: Starting With Matlab
Section: Chapter Questions
Problem 1P
Related questions
Question
![**Why Use an Alternative Formula for Sample Size in Confidence Intervals**
When calculating the sample size required to find a confidence interval for the population proportion, you might consider using the formula
\[ n \geq \frac{z_{\alpha/2}^2 \hat{p}(1 - \hat{p})}{h^2} \]
instead of
\[ n \geq \frac{z_{\alpha/2}^2}{4h^2} \]
**Explanation:**
The formula \( n \geq \frac{z_{\alpha/2}^2 \hat{p}(1 - \hat{p})}{h^2} \) allows for a more precise estimation as it incorporates the sample proportion \( \hat{p} \), making it more tailored to specific data when estimating the required sample size for a given confidence interval.
- **Variables:**
- \( z_{\alpha/2} \): Represents the z-score for the desired confidence level.
- \( \hat{p} \): Represents the sample proportion.
- \( h \): Reflects the amount of error you are willing to accept.
Using this formula can provide a more accurate sample size calculation based on the actual observed data, whereas the other formula is a more general calculation that assumes maximum variability in the proportion.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F0393b910-875a-4ed6-a578-5b5396be78bf%2F299e213b-f38d-4dfb-bc81-3129575a7ba3%2Flfci1_processed.png&w=3840&q=75)
Transcribed Image Text:**Why Use an Alternative Formula for Sample Size in Confidence Intervals**
When calculating the sample size required to find a confidence interval for the population proportion, you might consider using the formula
\[ n \geq \frac{z_{\alpha/2}^2 \hat{p}(1 - \hat{p})}{h^2} \]
instead of
\[ n \geq \frac{z_{\alpha/2}^2}{4h^2} \]
**Explanation:**
The formula \( n \geq \frac{z_{\alpha/2}^2 \hat{p}(1 - \hat{p})}{h^2} \) allows for a more precise estimation as it incorporates the sample proportion \( \hat{p} \), making it more tailored to specific data when estimating the required sample size for a given confidence interval.
- **Variables:**
- \( z_{\alpha/2} \): Represents the z-score for the desired confidence level.
- \( \hat{p} \): Represents the sample proportion.
- \( h \): Reflects the amount of error you are willing to accept.
Using this formula can provide a more accurate sample size calculation based on the actual observed data, whereas the other formula is a more general calculation that assumes maximum variability in the proportion.
Expert Solution
Step 1
when there is no prior estimate of the sample proportion (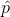
) is known, then we use,
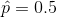
putting the value in the equation we have :-
Step by step
Solved in 2 steps with 5 images
Similar questions
Recommended textbooks for you
MATLAB: An Introduction with Applications
Statistics
ISBN:
9781119256830
Author:
Amos Gilat
Publisher:
John Wiley & Sons Inc
Probability and Statistics for Engineering and th…
Statistics
ISBN:
9781305251809
Author:
Jay L. Devore
Publisher:
Cengage Learning
Statistics for The Behavioral Sciences (MindTap C…
Statistics
ISBN:
9781305504912
Author:
Frederick J Gravetter, Larry B. Wallnau
Publisher:
Cengage Learning
MATLAB: An Introduction with Applications
Statistics
ISBN:
9781119256830
Author:
Amos Gilat
Publisher:
John Wiley & Sons Inc
Probability and Statistics for Engineering and th…
Statistics
ISBN:
9781305251809
Author:
Jay L. Devore
Publisher:
Cengage Learning
Statistics for The Behavioral Sciences (MindTap C…
Statistics
ISBN:
9781305504912
Author:
Frederick J Gravetter, Larry B. Wallnau
Publisher:
Cengage Learning
Elementary Statistics: Picturing the World (7th E…
Statistics
ISBN:
9780134683416
Author:
Ron Larson, Betsy Farber
Publisher:
PEARSON
The Basic Practice of Statistics
Statistics
ISBN:
9781319042578
Author:
David S. Moore, William I. Notz, Michael A. Fligner
Publisher:
W. H. Freeman
Introduction to the Practice of Statistics
Statistics
ISBN:
9781319013387
Author:
David S. Moore, George P. McCabe, Bruce A. Craig
Publisher:
W. H. Freeman