Do cars get better gas mileage on the highway?The table shows the mileage per gallon of cars on city streets and the mileage per gallon of cars on the highway. Assume that the two samples are randomly selected. At the 0.1 significance level, test the claim that the mean difference in miles per gallon is higher for cars on the city streets.(Be sure to subtract in the same direction). City (mpg)Highway (mpg)Difference (mpg)27.731.917.616.518.827.528.234.621.326.419.130.428.326.72024.1What are the correct hypotheses? (Select the correct symbols and values.)Ho: Select an answer? Select an answerH1: Select an answer v? v Select an answerOriginal ClaimSelect an answer vdf = Based on the hypotheses, find the following:Test Statistic =(Round to three decimal places.)Critical value(s) =(Round to three decimal places.)p-value =(Round to four decimal places.)Shade the sampling distribution curve with the correct critical value(s) and shade the critical regions. Thearrows can only be dragged to t-scores that are accurate to 1 place after the decimal point (these valuescorrespond to the tick marks on the horizontal axis). Select from the drop down menu to shade to the left,to the right, between or left and right of the t-score(s).Shade: Left of a valueClick and drag the arrows to adjust the values.-4-2-1234-1,5Decision: Select an answerConclusion: Select an answerv the claim that the mean difference inmiles per gallon is higher for cars on the city streets.

Name: Do cars get better gas mileage on the highway?The table shows the mile
Uploaded: 2024-03-20T07:07:12.000Z
Channel: Bartleby
Description: Do cars get better gas mileage on the highway?The table shows the mileage per gallon of cars on city streets and the mileage per gallon of cars on the highway. Assume that the two samples are randomly selected. At the 0.1 significance level, test the

Answered: Do cars get better gas mileage on the…

MATLAB: An Introduction with Applications

6th Edition

ISBN:9781119256830

Author:Amos Gilat

Publisher:Amos Gilat

Chapter1: Starting With Matlab

Section: Chapter Questions

Problem 1P

See similar textbooks

Related questions

Topic Video

Question

Do cars get better gas mileage on the highway?

The table shows the mileage per gallon of cars on city streets and the mileage per gallon of cars on the highway. Assume that the two samples are randomly selected. At the 0.1 significance level, test the claim that the mean difference in miles per gallon is higher for cars on the city streets.
(Be sure to subtract in the same direction).

City (mpg)
Highway (mpg)
Difference (mpg)
27.7
31.9
17.6
16.5
18.8
27.5
28.2
34.6
21.3
26.4
19.1
30.4
28.3
26.7
20
24.1
What are the correct hypotheses? (Select the correct symbols and values.)
Ho: Select an answer
? Select an answer
H1: Select an answer v
? v Select an answer
Original Claim
Select an answer v
df =

Based on the hypotheses, find the following:
Test Statistic =
(Round to three decimal places.)
Critical value(s) =
(Round to three decimal places.)
p-value =
(Round to four decimal places.)
Shade the sampling distribution curve with the correct critical value(s) and shade the critical regions. The
arrows can only be dragged to t-scores that are accurate to 1 place after the decimal point (these values
correspond to the tick marks on the horizontal axis). Select from the drop down menu to shade to the left,
to the right, between or left and right of the t-score(s).
Shade: Left of a value
Click and drag the arrows to adjust the values.
-4
-2
-1
2
3
4
-1,5
Decision: Select an answer
Conclusion: Select an answer
v the claim that the mean difference in
miles per gallon is higher for cars on the city streets.

Definition Definition Measure of central tendency that is the average of a given data set. The mean value is evaluated as the quotient of the sum of all observations by the sample size. The mean, in contrast to a median, is affected by extreme values. Very large or very small values can distract the mean from the center of the data. Arithmetic mean: The most common type of mean is the arithmetic mean. It is evaluated using the formula: μ = 1 N ∑ i = 1 N x i Other types of means are the geometric mean, logarithmic mean, and harmonic mean. Geometric mean: The nth root of the product of n observations from a data set is defined as the geometric mean of the set: G = x 1 x 2 ... x n n Logarithmic mean: The difference of the natural logarithms of the two numbers, divided by the difference between the numbers is the logarithmic mean of the two numbers. The logarithmic mean is used particularly in heat transfer and mass transfer. ln x 2 − ln x 1 x 2 − x 1 Harmonic mean: The inverse of the arithmetic mean of the inverses of all the numbers in a data set is the harmonic mean of the data. 1 1 x 1 + 1 x 2 + ...

Expert Solution

Step 1

Given that,

Sample size $n = 8$

The difference between two paired samples is calculated using formula $d = C i t y - H i g h w a y$ as follows:

City	Highway	Difference (d)
27.7	31.9	-4.20
17.6	16.5	1.10
18.8	27.5	-8.70
28.2	34.6	-6.40
21.3	26.4	-5.10
19.1	30.4	-11.3
28.3	26.7	2.00
20	24.1	-4.10

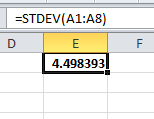
Mean and standard deviation of difference is calculated using EXCEL functions as given below:

Mean: “=AVERAGE (select array of data values)”

Standard deviation: “=STDEV (select array of data values)”

The mean of the difference is $\bar{d} = - 4.588$

Standard deviation of difference $s_{d} = 4.4984$

Step 2

Hypothesis:

$H_{0} : μ_{d} \leq 0$ (That is, the mean difference in miles per gallon is not higher for cars on the city streets.)

$H_{1} : μ_{d} > 0$ (That is, the mean difference in miles per gallon is higher for cars on the city streets.)

Degrees of freedom is $(n - 1) = 7$

Test Statistic:

The test statistic value can be obtained as follows:

$\begin{array}{rcl} t & = & \frac{\bar{d}}{\frac{s_{d}}{\sqrt{n}}} \\ = & \frac{- 4.588}{\frac{4.4984}{\sqrt{8}}} \\ = & - 2.885 \end{array}$

Step by step

Solved in 3 steps with 3 images

Knowledge Booster

$Hypothesis Tests and Confidence Intervals for Means$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.