**Problem Statement:**Determine the reactions hinges A and D exert on the frame and the force in each two-force member. (Assume that the +x-axis is to the right and the +y-axis is up along the page. Enter forces in pounds.)**Diagram:**The diagram presents a horizontal frame with a uniformly distributed load of 320 lb/ft acting across a 4-foot length from point B to point C. The frame is supported by hinges at points A and D. Distances are marked as follows:- From A to B: 2 ft- From B to C: 4 ft- From C to D: 2 ftVertical members E and F connect the horizontal beam to hinges A and D, respectively.**Force Calculations:**1. $ \vec{A}_x $ - Magnitude: 0 lb - Direction: The magnitude is zero.2. $ \vec{A}_y $ - Magnitude: [Enter a number] - Direction: [Selection required]3. $ \vec{D}_x $ - Magnitude: 0 lb - Direction: The magnitude is zero.4. $ \vec{D}_y $ - Magnitude: [Enter a number] - Direction: [Selection required]5. $ F_{BE} $ - Magnitude: [Enter a number] - Sense: Compression6. $ F_{CF} $ - Magnitude: [Enter a number] - Sense: Tension**Instructions:**- Input values for $ \vec{A}_y $, $ \vec{D}_y $, $ F_{BE} $, and $ F_{CF} $ using the appropriate sense (tension or compression) and consider the indicated direction for forces.- Calculate reactions considering equilibrium conditions for the system.

Answered: Determine the reactions hinges A and D…

Structural Analysis

6th Edition

ISBN:9781337630931

Author:KASSIMALI, Aslam.

Publisher:KASSIMALI, Aslam.

Chapter2: Loads On Structures

Section: Chapter Questions

Problem 1P

See similar textbooks

Related questions

Concept explainers

Question

**Problem Statement:**

Determine the reactions hinges A and D exert on the frame and the force in each two-force member. (Assume that the +x-axis is to the right and the +y-axis is up along the page. Enter forces in pounds.)

**Diagram:**

The diagram presents a horizontal frame with a uniformly distributed load of 320 lb/ft acting across a 4-foot length from point B to point C. The frame is supported by hinges at points A and D. Distances are marked as follows:
- From A to B: 2 ft
- From B to C: 4 ft
- From C to D: 2 ft

Vertical members E and F connect the horizontal beam to hinges A and D, respectively.

**Force Calculations:**

1. $ \vec{A}_x $
- Magnitude: 0 lb
- Direction: The magnitude is zero.

2. $ \vec{A}_y $
- Magnitude: [Enter a number]
- Direction: [Selection required]

3. $ \vec{D}_x $
- Magnitude: 0 lb
- Direction: The magnitude is zero.

4. $ \vec{D}_y $
- Magnitude: [Enter a number]
- Direction: [Selection required]

5. $ F_{BE} $
- Magnitude: [Enter a number]
- Sense: Compression

6. $ F_{CF} $
- Magnitude: [Enter a number]
- Sense: Tension

**Instructions:**

- Input values for $ \vec{A}_y $, $ \vec{D}_y $, $ F_{BE} $, and $ F_{CF} $ using the appropriate sense (tension or compression) and consider the indicated direction for forces.
- Calculate reactions considering equilibrium conditions for the system.

Expert Solution

Step 1

Member BCD.

The following figure shows the Free Body Diagram of Member BCD.

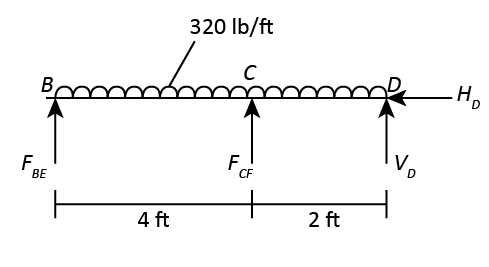
The number of unknowns in the beam is 4.

The number of available equilibrium equations is 3.

Since, the number of unknowns is more than the number of equilibrium equations, the beam is statically indeterminate.

Adopt Moment Distribution Method to solve the beam.

Calculate the Fixed End Moments.

The fixed end moments for beam subjected to uniformly distributed load is given by,

$M_{F} = \frac{w L^{2}}{12}$

Therefore, the fixed end moments for span BC is,

$\begin{array}{rcl} M_{F B C} & = & \frac{(320 lb/ft) \times {(4 ft)}^{2}}{12} \\ = & 426.67 lb-ft \\ M_{F C B} & = & - \frac{(320 lb/ft) \times {(4 ft)}^{2}}{12} \\ = & - 426.67 lb-ft \end{array}$

The fixed end moments for span CD is,

$\begin{array}{rcl} M_{F B C} & = & \frac{(320 lb/ft) \times {(2 ft)}^{2}}{12} \\ = & 106.67 lb-ft \\ M_{F C B} & = & - \frac{(320 lb/ft) \times {(2 ft)}^{2}}{12} \\ = & - 106.67 lb-ft \end{array}$

Calculate the distributing factors for the beam spans.

Point	Span	Stiffness	Total Stiffness	Distribution Factor
C	BC	3EI/4=0.75EI	2.25EI	0.33
	CD	3EI/2=1.5EI	2.25EI	0.67

Calculate the actual moments at the support

	BC	CB	CD	DC
Distribution Factors	-	0.33	0.67
Fixed End Moments	426.67	-426.67	106.67	-106.67
Adjustment of Moment at B and D	-426.67	-	-	+106.67
Carryover Moment	-	-213.33	+53.33	-
Total Moment	0	-640	160	0
Adjustment of Moment at B and C	0	+158.4	+321.6	0
Total Moment	0	-481.6	+481.6	0

Calculate Support Reactions.

Calculate Support reaction for Span BC.

The following figure shows the Free Body Diagram of the Span BC.

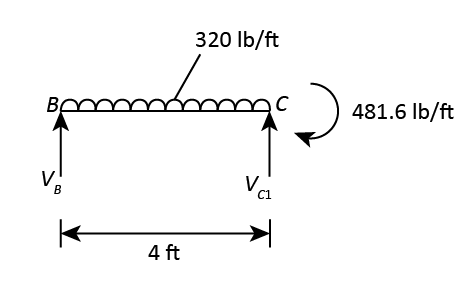
Consider moment of all the forces with respect to Point B.

Since the beam is in equilibrium, the sum of the moment at B will be zero.

$\begin{array}{rcl} M_{B} & = & 0 \\ V_{C 1} \times (4 ft) - (320 lb/ft) (4 ft) \times \frac{(4 ft)}{2} - (481.6 lb-ft) & = & 0 \\ 4 V_{C 1} - 2560 - 481.6 & = & 0 \\ V_{C 1} & = & \frac{3041.6}{4} \\ = & 760.4 lb \end{array}$

The sum of all the forces in Y-direction is zero.

$\begin{array}{rcl} F_{Y} & = & 0 \\ V_{B} + V_{C 1} - (320 lb/ft) \times (4 ft) & = & 0 \\ V_{B} + (760.4 lb) - (320 lb/ft) \times (4 ft) & = & 0 \\ V_{B} & = & 1280 - 760.4 \\ = & 519.6 lb \end{array}$

Calculate Support reaction for Span CD.

The following figure shows the Free Body Diagram of the Span CD.

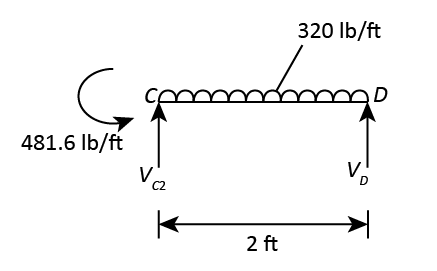
Consider moment of all the forces with respect to Point D.

Since the beam is in equilibrium, the sum of the moment at D will be zero.

$\begin{array}{rcl} M_{D} & = & 0 \\ V_{C 2} \times (2 ft) - (320 lb/ft) (2 ft) \times \frac{(2 ft)}{2} - (481.6 lb-ft) & = & 0 \\ 2 V_{C 2} - 640 - 481.6 & = & 0 \\ V_{C 2} & = & \frac{1121.6}{2} \\ = & 560.8 lb \end{array}$

The sum of all the forces in Y-direction is zero.

$\begin{array}{rcl} F_{Y} & = & 0 \\ V_{C 2} + V_{D} - (320 lb/ft) \times (2 ft) & = & 0 \\ (560.8 lb) + V_{D} - 640 & = & 0 \\ V_{D} & = & 79.2 lb \end{array}$

The sum of all the forces in X-direction is zero.

$\begin{array}{rcl} F_{X} & = & 0 \\ H_{D} & = & 0 \end{array}$

Step by step

Solved in 3 steps with 4 images

SEE SOLUTION Check out a sample Q&A here

Knowledge Booster

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, civil-engineering and related others by exploring similar questions and additional content below.