Definition Do the following.: Let f(x) be a function defined in an open interval containing a. The derivative of the function f(x) at a, denoted by f' (a), is defined by S" (a) = Jim f(x) – f(a) (3.5) Use limit definition (Formula 3.5 page 220 in the TextBook) to determine whether the function is differentiable at x = 2. 1. f(x) = |x – 2|.
Definition Do the following.: Let f(x) be a function defined in an open interval containing a. The derivative of the function f(x) at a, denoted by f' (a), is defined by S" (a) = Jim f(x) – f(a) (3.5) Use limit definition (Formula 3.5 page 220 in the TextBook) to determine whether the function is differentiable at x = 2. 1. f(x) = |x – 2|.
Chapter3: Functions
Section3.3: Rates Of Change And Behavior Of Graphs
Problem 2SE: If a functionfis increasing on (a,b) and decreasing on (b,c) , then what can be said about the local...
Related questions
Question
I do not understand how to solve this problem I need a step by step solution please.

Transcribed Image Text:Definition
6. Do the following. :
Let f(x) be a function defined in an open interval containing a. The derivative of the function f(x) at a, denoted
by f' (a), is defined by
f' (a) = lim
f(x) – f(a)
(3.5)
X- a
Use limit definition (Formula 3.5 page 220 in the TextBook) to determine
whether the function is differentiable at x = 2.
1. f(x) = |x – 2|.
Expert Solution
Step 1
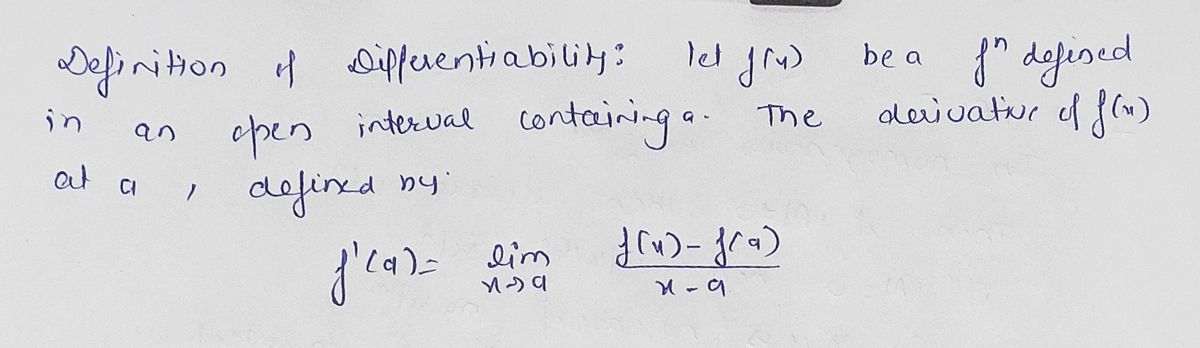
Step by step
Solved in 2 steps with 2 images

Similar questions
Recommended textbooks for you


College Algebra (MindTap Course List)
Algebra
ISBN:
9781305652231
Author:
R. David Gustafson, Jeff Hughes
Publisher:
Cengage Learning

College Algebra
Algebra
ISBN:
9781305115545
Author:
James Stewart, Lothar Redlin, Saleem Watson
Publisher:
Cengage Learning


College Algebra (MindTap Course List)
Algebra
ISBN:
9781305652231
Author:
R. David Gustafson, Jeff Hughes
Publisher:
Cengage Learning

College Algebra
Algebra
ISBN:
9781305115545
Author:
James Stewart, Lothar Redlin, Saleem Watson
Publisher:
Cengage Learning