D. (In this problem we show any square matrix is the sum of a symmetric matrix and a skew-symmetric matrix). Let A be a square matrix. From this define and C=(A-A¹). (a) Using general properties of the transpose, pg. 36, show B is symmetric, i.e. B = B. 1 B = (A + A¹) (b) Using general properties of the transpose, pg. 36, show C is skew-symmetric, i.e. Ct =-C. (c) Show B+C = A. (d) An example: for A = 1 2 34 compute B and C.
D. (In this problem we show any square matrix is the sum of a symmetric matrix and a skew-symmetric matrix). Let A be a square matrix. From this define and C=(A-A¹). (a) Using general properties of the transpose, pg. 36, show B is symmetric, i.e. B = B. 1 B = (A + A¹) (b) Using general properties of the transpose, pg. 36, show C is skew-symmetric, i.e. Ct =-C. (c) Show B+C = A. (d) An example: for A = 1 2 34 compute B and C.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
Question number 10 and 11
![10. (In this problem we show any square matrix is the sum of a symmetric matrix and a
skew-symmetric matrix).
Let A be a square matrix. From this define
and
=
(d) An example: for A
=
1 2
3 4
-
B
с
-
(a) Using general properties of the transpose, pg. 36, show B is symmetric, i.e.
Bt B.
7
2
=
1
(b) Using general properties of the transpose, pg. 36, show C is skew-symmetric, i.e.
Ct=-C.
(c) Show B+C = A.
(4+
(A + A¹)
2
1
(4-
(A – Aª).
11. For two nx n matrices A and B, we define the commutator, denoted [A, B], by
[A, B]
AB - BA.
a) What is [A, I], where I is the n x n identity matrix?
b) What is [A, A] for any n x n matrix A ?
c) Give an example of two nonzero 2 × 2 matrices A and B such that [A, B] is not the
zero matrix.
d) Fix an n x n matrix C. Show that [A + B, C] = [A, C] + [B, C]
e) [Optional but fun!] Compute out this sum
compute B and C.
[A, [B, C]] + [B, [C, A]] + [C, [A, B]].](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F8783cbc5-0f10-43ba-8bd7-4625ee264f91%2Feda1bdca-3ddb-4fb4-9735-f482733fd920%2Frt3bpob_processed.jpeg&w=3840&q=75)
Transcribed Image Text:10. (In this problem we show any square matrix is the sum of a symmetric matrix and a
skew-symmetric matrix).
Let A be a square matrix. From this define
and
=
(d) An example: for A
=
1 2
3 4
-
B
с
-
(a) Using general properties of the transpose, pg. 36, show B is symmetric, i.e.
Bt B.
7
2
=
1
(b) Using general properties of the transpose, pg. 36, show C is skew-symmetric, i.e.
Ct=-C.
(c) Show B+C = A.
(4+
(A + A¹)
2
1
(4-
(A – Aª).
11. For two nx n matrices A and B, we define the commutator, denoted [A, B], by
[A, B]
AB - BA.
a) What is [A, I], where I is the n x n identity matrix?
b) What is [A, A] for any n x n matrix A ?
c) Give an example of two nonzero 2 × 2 matrices A and B such that [A, B] is not the
zero matrix.
d) Fix an n x n matrix C. Show that [A + B, C] = [A, C] + [B, C]
e) [Optional but fun!] Compute out this sum
compute B and C.
[A, [B, C]] + [B, [C, A]] + [C, [A, B]].
Expert Solution
Step 1
As per our guideline, we are supposed to solve only first question. Kindly repost other question as next question.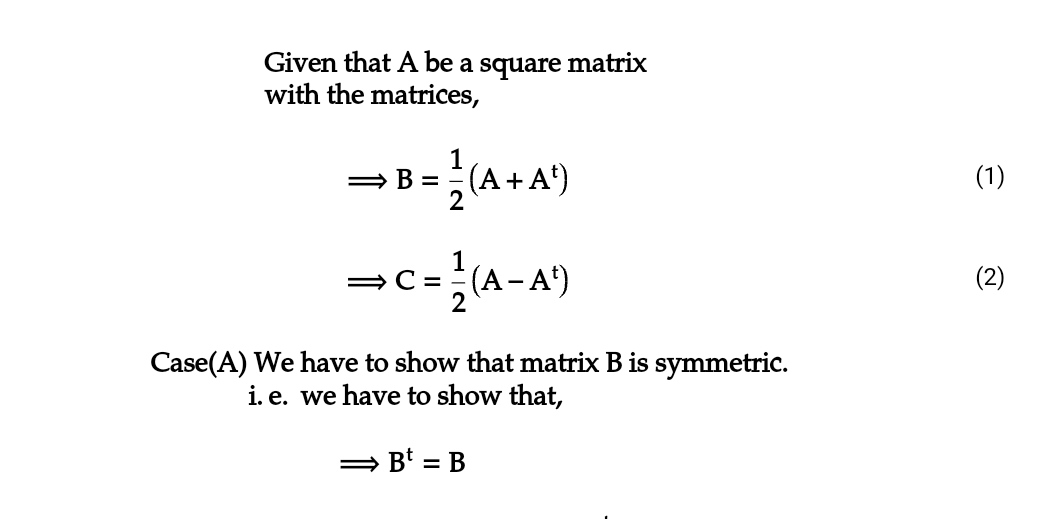
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

