Homework Help is Here – Start Your Trial Now!
Science
Physics
(d) If this changes takes place in some small At and if we divide both sides of the equation Avr = rAw by At, justify that we will get at = ra, where a is called the tangential acceleration and a is the rigid body angular acceleration. Most importantly, for example, this result tells us the relationship between the angular acceleration of the wheel of the car and the linear acceleration of the car. (e) When an object is under a rotational motion or circular motion, that object besides contains tangential acceleration it also has centripetal acceleration as well. In the figure below, for example, the child on the merry-go-round has both tangential and centripetal acceleration. The equation for the centripetal acceleration is a, = v7/r (we are not going to derive this equation), and its direction of acceleration is toward the center. Using Newton's second law, this gives the centripetal force as F = mag or Fep = . Does this make sense? What is the direction of the centripetal force on the child?

(d) If this changes takes place in some small At and if we divide both sides of the equation Avr = rAw by At, justify that we will get at = ra, where a is called the tangential acceleration and a is the rigid body angular acceleration. Most importantly, for example, this result tells us the relationship between the angular acceleration of the wheel of the car and the linear acceleration of the car. (e) When an object is under a rotational motion or circular motion, that object besides contains tangential acceleration it also has centripetal acceleration as well. In the figure below, for example, the child on the merry-go-round has both tangential and centripetal acceleration. The equation for the centripetal acceleration is a, = v7/r (we are not going to derive this equation), and its direction of acceleration is toward the center. Using Newton's second law, this gives the centripetal force as F = mag or Fep = . Does this make sense? What is the direction of the centripetal force on the child?

College Physics
College Physics
11th Edition
ISBN:9781305952300
Author:Raymond A. Serway, Chris Vuille
Publisher:Raymond A. Serway, Chris Vuille
Chapter1: Units, Trigonometry. And Vectors
Section: Chapter Questions
Problem 1CQ: Estimate the order of magnitude of the length, in meters, of each of the following; (a) a mouse, (b)...
See similar textbooks
icon
Related questions
Question

can you answer parts d and e please?

7. When a rigid body rotates about a fixed axis, every particle in the body moves in a circular path. As shown in the figure below, the arclength As between the angular positions 6, and 82 is given as As = rA8. Do you agree with this equation? rotational motion (a) In the limit where A6 is very small, then As can be consider as a straight line. Is this true or false? AsrAe (b) It follows from statement (a) that any points along the circular path there is a tangential velocity (vr) that is always perpendicular to the radius of the rotating body. Hence, if we divide both sides of the equation As = rAe by At, justify that we will get v = rw. This result indicates that the direction of the particle's velocity is tangential to its circular path at each point. Most importantly, for example, this result tells us the relation- ship between the angular velocity of the wheel of the car and linear velocity of the car. Reference line At (c) If the angular velocity changes by Aw, then the rotating object's linear speed will change by Avr. Hence, we will have Aer = rAw. Is this a true statement? (d) If this changes takes place in some small At and if we divide both sides of the equation Av = rAw by At, justify that we will get at = ra, where a is called the tangential acceleration and a is the rigid body angular acceleration. Most importantly, for example, this result tells us the relationship between the angular acceleration of the wheel of the car and the linear acceleration of the car. (e) When an object is under a rotational motion or circular motion, that object besides contains tangential acceleration it also has centripetal acceleration as well. In the figure below, for example, the child on the merry-go-round has both tangential and centripetal acceleration. The equation for the centripetal acceleration is ap = v7/r (we are not going to derive this equation), and its direction of acceleration is toward the center. Using Newton's second law, this gives the centripetal force as Fep = map or Fep = . Does this make sense? What is the direction of the centripetal force on the child?
Transcribed Image Text:7. When a rigid body rotates about a fixed axis, every particle in the body moves in a circular path. As shown in the figure below, the arclength As between the angular positions 6, and 82 is given as As = rA8. Do you agree with this equation? rotational motion (a) In the limit where A6 is very small, then As can be consider as a straight line. Is this true or false? AsrAe (b) It follows from statement (a) that any points along the circular path there is a tangential velocity (vr) that is always perpendicular to the radius of the rotating body. Hence, if we divide both sides of the equation As = rAe by At, justify that we will get v = rw. This result indicates that the direction of the particle's velocity is tangential to its circular path at each point. Most importantly, for example, this result tells us the relation- ship between the angular velocity of the wheel of the car and linear velocity of the car. Reference line At (c) If the angular velocity changes by Aw, then the rotating object's linear speed will change by Avr. Hence, we will have Aer = rAw. Is this a true statement? (d) If this changes takes place in some small At and if we divide both sides of the equation Av = rAw by At, justify that we will get at = ra, where a is called the tangential acceleration and a is the rigid body angular acceleration. Most importantly, for example, this result tells us the relationship between the angular acceleration of the wheel of the car and the linear acceleration of the car. (e) When an object is under a rotational motion or circular motion, that object besides contains tangential acceleration it also has centripetal acceleration as well. In the figure below, for example, the child on the merry-go-round has both tangential and centripetal acceleration. The equation for the centripetal acceleration is ap = v7/r (we are not going to derive this equation), and its direction of acceleration is toward the center. Using Newton's second law, this gives the centripetal force as Fep = map or Fep = . Does this make sense? What is the direction of the centripetal force on the child?
Expert Solution
Step 1

d)

The given equation is,

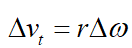
Physics homework question answer, step 1, image 1

Here, Δvt, r, and Δω represent the change in the tangential velocity, the circular path’s radius, and the change in angular velocity, respectively.

Dividing both sides by a small-time interval Δt.

Thus,

Physics homework question answer, step 1, image 2

Now, for the time interval to be very small, that is, approaching 0,

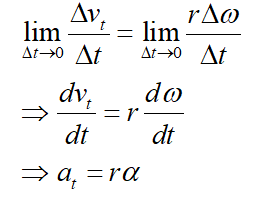
Physics homework question answer, step 1, image 3

Here, at and α represent the tangential acceleration, and angular acceleration, respectively.

steps

Step by step

Solved in 2 steps with 7 images

Blurred answer
Knowledge Booster
Vector basics
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.
Recommended textbooks for you
College Physics
College Physics
Physics
ISBN:
9781305952300
Author:
Raymond A. Serway, Chris Vuille
Publisher:
Cengage Learning
University Physics (14th Edition)
University Physics (14th Edition)
Physics
ISBN:
9780133969290
Author:
Hugh D. Young, Roger A. Freedman
Publisher:
PEARSON
Introduction To Quantum Mechanics
Introduction To Quantum Mechanics
Physics
ISBN:
9781107189638
Author:
Griffiths, David J., Schroeter, Darrell F.
Publisher:
Cambridge University Press
Physics for Scientists and Engineers
Physics for Scientists and Engineers
Physics
ISBN:
9781337553278
Author:
Raymond A. Serway, John W. Jewett
Publisher:
Cengage Learning
Lecture- Tutorials for Introductory Astronomy
Lecture- Tutorials for Introductory Astronomy
Physics
ISBN:
9780321820464
Author:
Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina Brissenden
Publisher:
Addison-Wesley
College Physics: A Strategic Approach (4th Editio…
College Physics: A Strategic Approach (4th Editio…
Physics
ISBN:
9780134609034
Author:
Randall D. Knight (Professor Emeritus), Brian Jones, Stuart Field
Publisher:
PEARSON
SEE MORE TEXTBOOKS