Create a 99% Confidence interval for the mean. Provide a sketch of the critical value and calculate the standard error. Only for this part use o = 23.8


Here you're given the following data set.
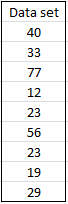
Given :
- Population standard deviation , σ = 23.8.
And asked to find
- 99% confidence interval for mean.
- The standard error value.
Note : Here population standard deviation (σ) is given , we will use z critical value to find the confidence interval.
The formula for a 99% confidence interval is as follows.
Where ,
- x̅ = Sample mean.
- z' = Critical value for the given confidence level.
- σ = Population standard deviation.
- n = Sample size.
Let's start to find one by one.
n = Number of numbers in your data set and it is equal to 9.
σ = 23.8
x̅ = 34.67 [ using the MS-EXCEL function = Average (number1 , number2 , ..... , number 9].
To find critical value , z' we need to find area 1 − and then use MS-Excel to find critical value.
We know that given confidence level = 0.99
From this , significance level , α = 1 - c = 1 - 0.99 = 0.01.
Thus ,
Now for this area = 0.995 we have to find critical value.
We can easily find this critical value by using MS-excel function = NORMSINV(0.995).
and it will return 2.575829 up to two decimal places it would be 2.58.
Thus , critical value , z' = 2.58.
Step by step
Solved in 6 steps with 2 images









