Constructing a Confidence Interval for a Population Mean You measure 32 textbooks' weights, and find they have a mean weight of 52 ounces. Assume the population standard deviation is 10.7 ounces. Based on this, construct a 95% confidence interval for the true population mean textbook weight. Give your answers as decimals, rounded to two decimal places.
Constructing a Confidence Interval for a Population Mean You measure 32 textbooks' weights, and find they have a mean weight of 52 ounces. Assume the population standard deviation is 10.7 ounces. Based on this, construct a 95% confidence interval for the true population mean textbook weight. Give your answers as decimals, rounded to two decimal places.
MATLAB: An Introduction with Applications
6th Edition
ISBN:9781119256830
Author:Amos Gilat
Publisher:Amos Gilat
Chapter1: Starting With Matlab
Section: Chapter Questions
Problem 1P
Related questions
Question
![**Constructing a Confidence Interval for a Population Mean**
You measure 32 textbooks' weights and find they have a mean weight of 52 ounces. Assume the population standard deviation is 10.7 ounces. Based on this, construct a 95% confidence interval for the true population mean textbook weight.
Give your answers as decimals, rounded to two decimal places.
**[Input box]** < µ < **[Input box]**
---
To solve this, use the formula for the confidence interval for a population mean when the population standard deviation is known:
\[
\text{Confidence Interval} = \bar{x} \pm Z \left(\frac{\sigma}{\sqrt{n}}\right)
\]
Where:
- \(\bar{x}\) = sample mean = 52 ounces
- \(Z\) = Z-score corresponding to the desired confidence level (for 95%, \(Z \approx 1.96\))
- \(\sigma\) = population standard deviation = 10.7 ounces
- \(n\) = sample size = 32
Calculate the margin of error and then determine the interval.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F5b06cc1a-670c-4da3-86c8-aa55d4f56c06%2F7cfd0935-d5cf-4581-8d94-1ffa815791b1%2F1vhjfy_processed.jpeg&w=3840&q=75)
Transcribed Image Text:**Constructing a Confidence Interval for a Population Mean**
You measure 32 textbooks' weights and find they have a mean weight of 52 ounces. Assume the population standard deviation is 10.7 ounces. Based on this, construct a 95% confidence interval for the true population mean textbook weight.
Give your answers as decimals, rounded to two decimal places.
**[Input box]** < µ < **[Input box]**
---
To solve this, use the formula for the confidence interval for a population mean when the population standard deviation is known:
\[
\text{Confidence Interval} = \bar{x} \pm Z \left(\frac{\sigma}{\sqrt{n}}\right)
\]
Where:
- \(\bar{x}\) = sample mean = 52 ounces
- \(Z\) = Z-score corresponding to the desired confidence level (for 95%, \(Z \approx 1.96\))
- \(\sigma\) = population standard deviation = 10.7 ounces
- \(n\) = sample size = 32
Calculate the margin of error and then determine the interval.
Expert Solution
Step 1
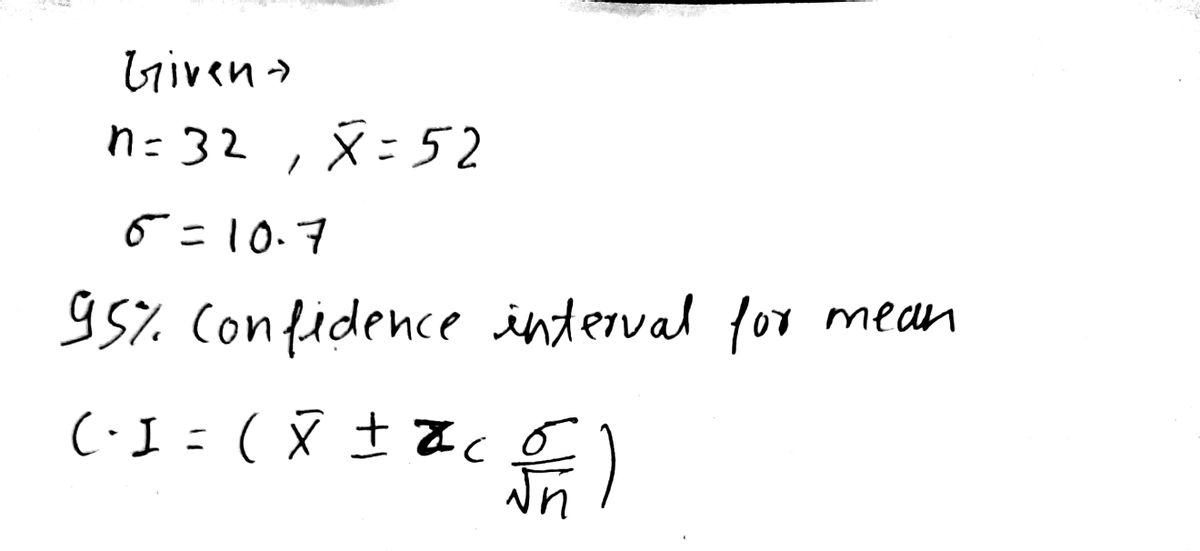
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

MATLAB: An Introduction with Applications
Statistics
ISBN:
9781119256830
Author:
Amos Gilat
Publisher:
John Wiley & Sons Inc

Probability and Statistics for Engineering and th…
Statistics
ISBN:
9781305251809
Author:
Jay L. Devore
Publisher:
Cengage Learning

Statistics for The Behavioral Sciences (MindTap C…
Statistics
ISBN:
9781305504912
Author:
Frederick J Gravetter, Larry B. Wallnau
Publisher:
Cengage Learning

MATLAB: An Introduction with Applications
Statistics
ISBN:
9781119256830
Author:
Amos Gilat
Publisher:
John Wiley & Sons Inc

Probability and Statistics for Engineering and th…
Statistics
ISBN:
9781305251809
Author:
Jay L. Devore
Publisher:
Cengage Learning

Statistics for The Behavioral Sciences (MindTap C…
Statistics
ISBN:
9781305504912
Author:
Frederick J Gravetter, Larry B. Wallnau
Publisher:
Cengage Learning

Elementary Statistics: Picturing the World (7th E…
Statistics
ISBN:
9780134683416
Author:
Ron Larson, Betsy Farber
Publisher:
PEARSON

The Basic Practice of Statistics
Statistics
ISBN:
9781319042578
Author:
David S. Moore, William I. Notz, Michael A. Fligner
Publisher:
W. H. Freeman

Introduction to the Practice of Statistics
Statistics
ISBN:
9781319013387
Author:
David S. Moore, George P. McCabe, Bruce A. Craig
Publisher:
W. H. Freeman