Consider two waves which, at time zero, match the two waves in the previous part. But thepurple wave, although it initially matches the black wave, moves to the right at a speed of 2units per second. Any reference to constructive or deconstructive interference refers specificallyto what happens at the origin.a) Write the new equation for the black wave that includes the motion. Now write thefunctional form of the wave formed by superposition of the orange and purple waves.Show any worked required to obtain these answers.b) At t=0, are the orange and purple waves interfering constructively or destructively?c) At what value of time, te, does maximal constructive interference happen? (Note you onlyneed to give the first time this occurs.) What is the resulting amplitude at the origin at thistime?d) At what time, ta, does the maximal deconstructive interference occur? (Note you onlyneed to give the first time this occurs.) What is the amplitude at the origin?e) Try to come up with a linear function, f, to quantify the amount of constructive anddeconstructive interference. Your answer should depend only on the amplitude of thewave at the origin, which we'll refer to as A(t). Specifically, construct a function f(A(t))where f(A(to))=1 and f(A(ta))=-1.f) Using your function from part (e), determine the resulting value at t=0. Briefly explainwhy your answer makes sense. 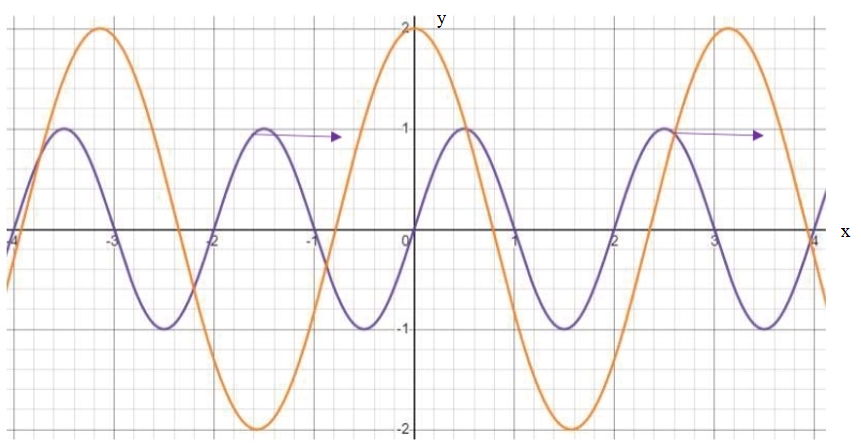Consider the follow image of two waves (i.e., orange and black oscillatory curves). Note that thehorizontal and vertical axes labels are the numbers on the straight lines intersecting at 0,0.a) What is the amplitude and wavelength of the black and orange lines? (Note the wavelengthmay be a whole number or a multiple of pi.)b) Write out the form of these two waves in terms of a sine or a cosine function times aconstant (i.e. in form Asin(cx) or Acos(cx) ).c) What is the momentum of a photon associated with each of the two waves? You mayassume the x-axis measures distance in units of nanometers.

Answered: Consider two waves which, at time zero,…

Similar questions

Sketch the resultant wave when the two traveling wave pulses in the figure interact, specifically when point A on the left wave is at the same position as point B on the right wave. Identify areas as constructive or destructive interference.
Public television station KQED in San Francisco broadcasts a sinusoidal radio signal at a power of 316 kW. Assume that the wave spreads out uniformly into a hemisphere above the ground. At a home 4.00 km away from the antenna, what average pressure does this wave exert on a totally reflecting surface? Pau 2.10x10-11 Pa Submit Previous Answers Part B Correct At a home 4.00 km away from the antenna, what are the amplitudes of the electric and magnetic fields of the wave? Emaz. Bmaz 1.54,5.13×10-9 N/C,T Submit Previous Answers Part C Correct At a home 4.00 km away from the antenna, what is the average density of the energy this wave carries? Ο ΑΣΦ ? that = 3.77.109 Submit Previous Answers Request Answer * Incorrect; Try Again; 4 attempts remaining Part D J/m³ For the energy density in part (c), what percentage is due to the electric field? 50.0 % Submit Previous Answers Part E Correct For the energy density in part (c), what percentage is due to the magnetic field? 50.0 % Submit Previous…
Needs Complete typed solution with 100 % accuracy.
Needs Complete solution with 100 % accuracy.
2. Consider the following diagram showing the crossing of two individual wave packets. Which phases represent total constructive interference? Which phases represent total destructive interference? a. Imagine that these two waves are water waves. If you were observing these waves on a pond, what would the water look like in phase E? What about in phase G? (Hint: Think about the sum of the two waves, and sketch what that sum would look like. Ask yourself, are the waves adding together, or canceling each other out?) b. Now imagine these two waves are light waves. In which phases would the interfering light waves appear brightest? In which phases would they appear the dimmest? A B C D E F G Figure 1: Crossing of two individual wave packets.
Please download the following worksheets, which show 4 separate grids. Each grid has two different waves (e.g., Wave and Wave B). Your goal is to draw the resulting wave (i.e., Wave C) if the two waves would have been superposed on top of each other. To do this, you'll need to add the two amplitudes (height of the Wave A and Wave B on the y-axis) at a given point on the x-axis to get the resulting one. For example, using number 3 as an example: a. At point 0 on the x axis, Wave A has an amplitude of 0, and Wave B has an amplitude of 0, so Wave C at point 0 would be 0. b. At point 4 on the x axis, Wave A has an amplitude of 6, and Wave B has an amplitude of 4, so Wave C at point 3 would have an amplitude of 10. c. At point 8 on the x axis. Wave A has an amplitdue of 0, and Wave B has an amplitude of -4, so Wave C at point 8 would be -4. You do not have to find the points for every single point along the x-axis, but just enough to get the general shape of the resulting wave. Once you…
Water waves from a source far to the left (not shown) travel in the rightward direction and disturb the height of the water by a maximum displacement A from the equilibrium level (dashed line). Mo the Marmot sits on a boat, which goes up and down as the traveling harmonic water wave passes by. Figure 1 shows a snapshot of this at some time. Figure 2 shows measurements of the vertical displacement from equilibrium, y, of Mo's boat as a function of time, which he recorded with his ioLab device. Figure 1 Figure 2 height [meters] y (meters) wave propagation direction At I (seconds] 2 3 4 -50 -40 -30 -20 -10 10 20 x (meters] What is the speed of the wave propagation? 60 m/s 1.1 m/s 6.7 m/s 42 m/s 260 m/s Which of the following equations best describes the displacement of the water surface from equilibrium, y, at a position a and a time t? y(x, t) = -A cos(kx – wt – 4) y(x, t) = -A cos(kx + wt + 4) %3D O y(x,t) = A cos(kæ + wt)