Consider the function f(x) = x2 The goal is to find a general formula for the area under this curve on the interval [0, b]. (a) Start by looking at finding the area under the graph of f(x) on [0, 1] using N rectangles, using the right endpoints as the test points. What do the endpoints look like? Use this to write the approximate area in summation notation. (b) What if this is done on [0, 2], still using N rectangles? How does this change the formulas and the sum? What are the right endpoints here? (c) What if this also done on [0, b] for some positive number b using N rectangles? What are the endpoints here? (d) With this last sum, expand things out and use the power sum rules to get this to an expression only depending on N. (e) Take the limit as N → ∞ to get the area under the graph of f(x) over [0, b].
Consider the function f(x) = x2
The goal is to find a general formula for the area under this curve on
the interval [0, b].
(a) Start by looking at finding the area under the graph of f(x) on [0, 1] using N rectangles, using the right endpoints as the test points. What do the endpoints look like? Use this to write the approximate area in summation notation.
(b) What if this is done on [0, 2], still using N rectangles? How does this change the formulas and the sum? What are the right endpoints here?
(c) What if this also done on [0, b] for some positive number b using N rectangles? What are the endpoints here?
(d) With this last sum, expand things out and use the power
(e) Take the limit as N → ∞ to get the area under the graph of f(x) over [0, b].
Hello. Since your question has multiple sub-parts, we will solve first three sub-parts for you. If you want remaining sub-parts to be solved, then please resubmit the whole question and specify those sub-parts you want us to solve.
Consider the given function.
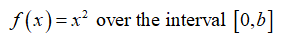
For part (a) it is required to it is required to write the approximated area in summation notation.
Trending now
This is a popular solution!
Step by step
Solved in 4 steps with 4 images









