Homework Help is Here – Start Your Trial Now!
Science
Physics
Consider an electric circuit containing a capacitor, resistor, and

Consider an electric circuit containing a capacitor, resistor, and

College Physics
College Physics
11th Edition
ISBN:9781305952300
Author:Raymond A. Serway, Chris Vuille
Publisher:Raymond A. Serway, Chris Vuille
Chapter1: Units, Trigonometry. And Vectors
Section: Chapter Questions
Problem 1CQ: Estimate the order of magnitude of the length, in meters, of each of the following; (a) a mouse, (b)...
See similar textbooks
icon
Related questions
Question

13 pl

a. If 100 mg of thorium-234 decays to 82.04 mg in 1 week. determine the decay rate r. b. Find an expression for the amount of thorium-234 present at any time t. c. Find the time required for the thorium-234 to decay to one- half its original amount. 11. The half-life of a radioactive material is the time required for an amount of this material to decay to one-half its original value. Show that for any radioactive material that decays according to the equation Q-rQ, the half-life 7 and the decay rate r satisfy the equation rt = ln 2. 12. According to Newton's law of cooling (see Problem 19 of Section 1.1), the temperature u(t) of an object satisfies the differential equation du dt = -k(u-T), where T is the constant ambient temperature and k is a positive constant. Suppose that the initial temperature of the object is u(0) = <= 10- a. Find the temperature of the object at any time. b. Let 7 be the time at which the initial temperature difference uo - T has been reduced by half. Find the relation between k and T. 13. Consider an electric circuit containing a capacitor, resistor, and N 14. A of a certain Water contai a rate of 300 rate. Assume pond. 1.3 5 a. Let t. Write b. Sol in the p c. At is rem mixtur initial d. So remain begin e. H G f. This equat 3.7. Classification The main purposes of this book are to di equations and to present some of the m or, in some cases, in approximating we describe here several useful ways vocabulary is essential to selecting app of solutions of differential equations
Transcribed Image Text:a. If 100 mg of thorium-234 decays to 82.04 mg in 1 week. determine the decay rate r. b. Find an expression for the amount of thorium-234 present at any time t. c. Find the time required for the thorium-234 to decay to one- half its original amount. 11. The half-life of a radioactive material is the time required for an amount of this material to decay to one-half its original value. Show that for any radioactive material that decays according to the equation Q-rQ, the half-life 7 and the decay rate r satisfy the equation rt = ln 2. 12. According to Newton's law of cooling (see Problem 19 of Section 1.1), the temperature u(t) of an object satisfies the differential equation du dt = -k(u-T), where T is the constant ambient temperature and k is a positive constant. Suppose that the initial temperature of the object is u(0) = <= 10- a. Find the temperature of the object at any time. b. Let 7 be the time at which the initial temperature difference uo - T has been reduced by half. Find the relation between k and T. 13. Consider an electric circuit containing a capacitor, resistor, and N 14. A of a certain Water contai a rate of 300 rate. Assume pond. 1.3 5 a. Let t. Write b. Sol in the p c. At is rem mixtur initial d. So remain begin e. H G f. This equat 3.7. Classification The main purposes of this book are to di equations and to present some of the m or, in some cases, in approximating we describe here several useful ways vocabulary is essential to selecting app of solutions of differential equations
a. If 100 mg of thorium-234 decays to 82.04 mg in 1 week. determine the decay rate r. b. Find an expression for the amount of thorium-234 present at any time t. c. Find the time required for the thorium-234 to decay to one- half its original amount. 11. The half-life of a radioactive material is the time required for an amount of this material to decay to one-half its original value. Show that for any radioactive material that decays according to the equation Q-rQ, the half-life 7 and the decay rate r satisfy the equation rt = ln 2. 12. According to Newton's law of cooling (see Problem 19 of Section 1.1), the temperature u(t) of an object satisfies the differential equation du dt = -k(u-T), where T is the constant ambient temperature and k is a positive constant. Suppose that the initial temperature of the object is u(0) = <= 10- a. Find the temperature of the object at any time. b. Let 7 be the time at which the initial temperature difference uo - T has been reduced by half. Find the relation between k and T. 13. Consider an electric circuit containing a capacitor, resistor, and N 14. A of a certain Water contai a rate of 300 rate. Assume pond. 1.3 5 a. Let t. Write b. Sol in the p c. At is rem mixtur initial d. So remain begin e. H G f. This equat 3.7. Classification The main purposes of this book are to di equations and to present some of the m or, in some cases, in approximating we describe here several useful ways vocabulary is essential to selecting app of solutions of differential equations
Transcribed Image Text:a. If 100 mg of thorium-234 decays to 82.04 mg in 1 week. determine the decay rate r. b. Find an expression for the amount of thorium-234 present at any time t. c. Find the time required for the thorium-234 to decay to one- half its original amount. 11. The half-life of a radioactive material is the time required for an amount of this material to decay to one-half its original value. Show that for any radioactive material that decays according to the equation Q-rQ, the half-life 7 and the decay rate r satisfy the equation rt = ln 2. 12. According to Newton's law of cooling (see Problem 19 of Section 1.1), the temperature u(t) of an object satisfies the differential equation du dt = -k(u-T), where T is the constant ambient temperature and k is a positive constant. Suppose that the initial temperature of the object is u(0) = <= 10- a. Find the temperature of the object at any time. b. Let 7 be the time at which the initial temperature difference uo - T has been reduced by half. Find the relation between k and T. 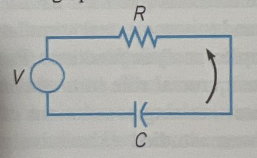13. Consider an electric circuit containing a capacitor, resistor, and N 14. A of a certain Water contai a rate of 300 rate. Assume pond. 1.3 5 a. Let t. Write b. Sol in the p c. At is rem mixtur initial d. So remain begin e. H G f. This equat 3.7. Classification The main purposes of this book are to di equations and to present some of the m or, in some cases, in approximating we describe here several useful ways vocabulary is essential to selecting app of solutions of differential equations
Expert Solution
Step 1

Given: 

RC circuit: 

Physics homework question answer, step 1, image 1

steps

Step by step

Solved in 3 steps with 3 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Knowledge Booster
Combination of resistance
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.
Recommended textbooks for you
College Physics
College Physics
Physics
ISBN:
9781305952300
Author:
Raymond A. Serway, Chris Vuille
Publisher:
Cengage Learning
University Physics (14th Edition)
University Physics (14th Edition)
Physics
ISBN:
9780133969290
Author:
Hugh D. Young, Roger A. Freedman
Publisher:
PEARSON
Introduction To Quantum Mechanics
Introduction To Quantum Mechanics
Physics
ISBN:
9781107189638
Author:
Griffiths, David J., Schroeter, Darrell F.
Publisher:
Cambridge University Press
Physics for Scientists and Engineers
Physics for Scientists and Engineers
Physics
ISBN:
9781337553278
Author:
Raymond A. Serway, John W. Jewett
Publisher:
Cengage Learning
Lecture- Tutorials for Introductory Astronomy
Lecture- Tutorials for Introductory Astronomy
Physics
ISBN:
9780321820464
Author:
Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina Brissenden
Publisher:
Addison-Wesley
College Physics: A Strategic Approach (4th Editio…
College Physics: A Strategic Approach (4th Editio…
Physics
ISBN:
9780134609034
Author:
Randall D. Knight (Professor Emeritus), Brian Jones, Stuart Field
Publisher:
PEARSON
SEE MORE TEXTBOOKS