Homework Help is Here – Start Your Trial Now!
Engineering
Electrical Engineering
Consider a transfer function given by G(s) = 1/(s+1). What is the gain (in dB) at the input frequency of 2.0 Hz that is predicted by the asymptotic approximation? Keep three significant figures.

Consider a transfer function given by G(s) = 1/(s+1). What is the gain (in dB) at the input frequency of 2.0 Hz that is predicted by the asymptotic approximation? Keep three significant figures.

Introductory Circuit Analysis (13th Edition)
Introductory Circuit Analysis (13th Edition)
13th Edition
ISBN:9780133923605
Author:Robert L. Boylestad
Publisher:Robert L. Boylestad
Chapter1: Introduction
Section: Chapter Questions
Problem 1P: Visit your local library (at school or home) and describe the extent to which it provides literature...
See similar textbooks
icon
Related questions
Question
SOLVE CAREFULLY!! Please Write Clearly and Box the final Answer Hint : Pay attention to values given
**Problem Statement:** Consider a transfer function given by \( G(s) = \frac{1}{(s+1)} \). What is the gain (in dB) at the input frequency of 2.0 Hz that is predicted by the asymptotic approximation? Keep three significant figures. [ **Answer Box:** ] **Explanation:** The problem involves calculating the gain in decibels (dB) for a given transfer function \( G(s) \) at a specified input frequency. The transfer function provided is \( G(s) = \frac{1}{(s+1)} \), where \( s \) represents the complex frequency variable. To find the gain in dB at 2.0 Hz using the asymptotic approximation, you would typically convert the frequency to the complex \( s \)-domain by using \( s = j\omega \), where \( \omega \) is the angular frequency (\( \omega = 2\pi f \) and \( f = 2.0 \) Hz). Follow these steps: 1. Substitute \( s = j\omega \) into the transfer function. 2. Calculate the magnitude of \( G(j\omega) \). 3. Convert the magnitude to decibels using the formula \( \text{Gain (dB)} = 20 \log_{10}(\text{Magnitude}) \). 4. Use asymptotic approximation methods if specified. The numerical calculations and asymptotic approximations are typically executed in computational exercises or systems analysis contexts.
Transcribed Image Text:**Problem Statement:** Consider a transfer function given by \( G(s) = \frac{1}{(s+1)} \). What is the gain (in dB) at the input frequency of 2.0 Hz that is predicted by the asymptotic approximation? Keep three significant figures. [ **Answer Box:** ] **Explanation:** The problem involves calculating the gain in decibels (dB) for a given transfer function \( G(s) \) at a specified input frequency. The transfer function provided is \( G(s) = \frac{1}{(s+1)} \), where \( s \) represents the complex frequency variable. To find the gain in dB at 2.0 Hz using the asymptotic approximation, you would typically convert the frequency to the complex \( s \)-domain by using \( s = j\omega \), where \( \omega \) is the angular frequency (\( \omega = 2\pi f \) and \( f = 2.0 \) Hz). Follow these steps: 1. Substitute \( s = j\omega \) into the transfer function. 2. Calculate the magnitude of \( G(j\omega) \). 3. Convert the magnitude to decibels using the formula \( \text{Gain (dB)} = 20 \log_{10}(\text{Magnitude}) \). 4. Use asymptotic approximation methods if specified. The numerical calculations and asymptotic approximations are typically executed in computational exercises or systems analysis contexts.
Expert Solution
Step 1

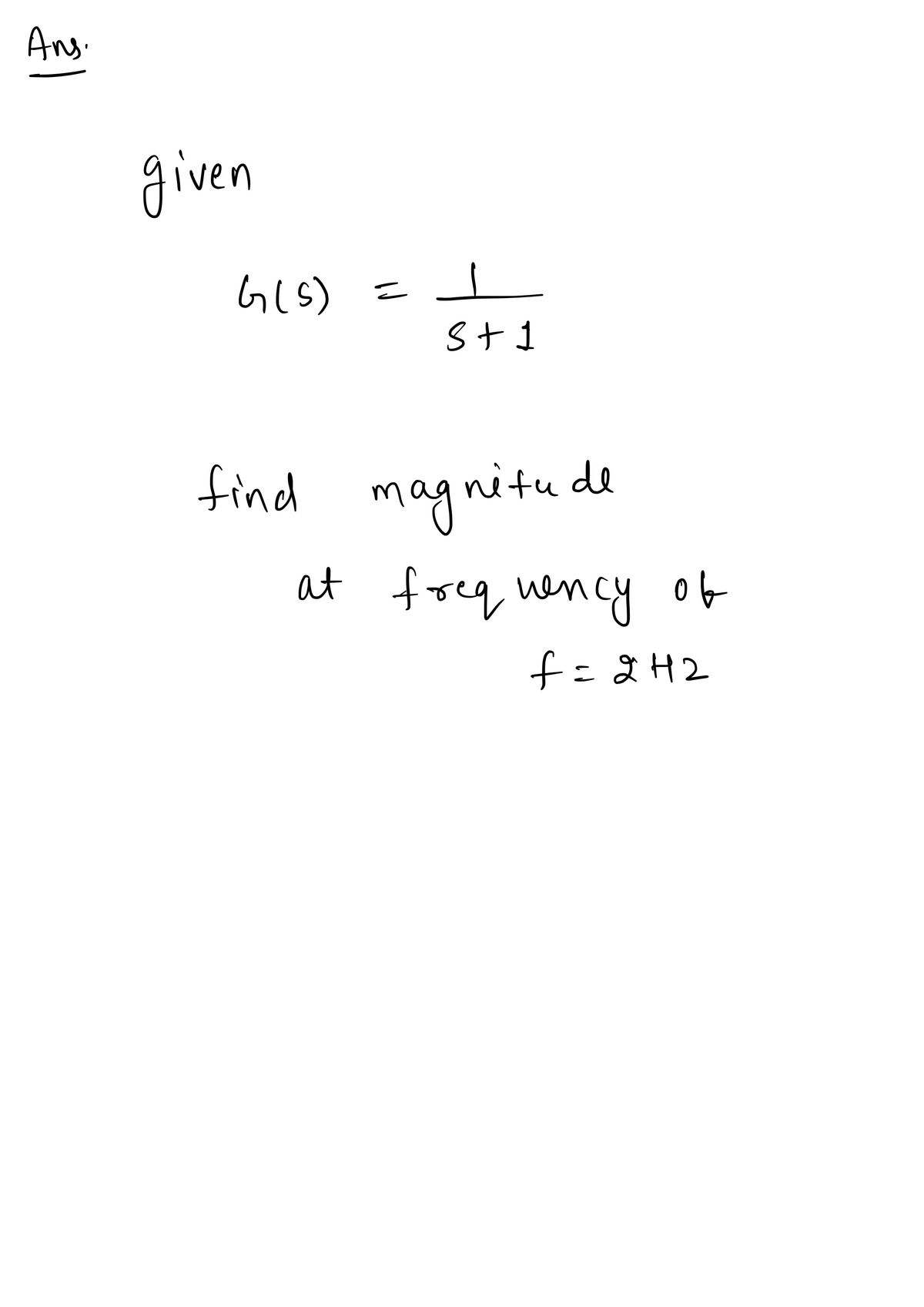
Electrical Engineering homework question answer, step 1, image 1

steps

Step by step

Solved in 2 steps with 2 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Knowledge Booster
Multistage amplifier
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, electrical-engineering and related others by exploring similar questions and additional content below.
Recommended textbooks for you
Introductory Circuit Analysis (13th Edition)
Introductory Circuit Analysis (13th Edition)
Electrical Engineering
ISBN:
9780133923605
Author:
Robert L. Boylestad
Publisher:
PEARSON
Delmar's Standard Textbook Of Electricity
Delmar's Standard Textbook Of Electricity
Electrical Engineering
ISBN:
9781337900348
Author:
Stephen L. Herman
Publisher:
Cengage Learning
Programmable Logic Controllers
Programmable Logic Controllers
Electrical Engineering
ISBN:
9780073373843
Author:
Frank D. Petruzella
Publisher:
McGraw-Hill Education
Fundamentals of Electric Circuits
Fundamentals of Electric Circuits
Electrical Engineering
ISBN:
9780078028229
Author:
Charles K Alexander, Matthew Sadiku
Publisher:
McGraw-Hill Education
Electric Circuits. (11th Edition)
Electric Circuits. (11th Edition)
Electrical Engineering
ISBN:
9780134746968
Author:
James W. Nilsson, Susan Riedel
Publisher:
PEARSON
Engineering Electromagnetics
Engineering Electromagnetics
Electrical Engineering
ISBN:
9780078028151
Author:
Hayt, William H. (william Hart), Jr, BUCK, John A.
Publisher:
Mcgraw-hill Education,
SEE MORE TEXTBOOKS