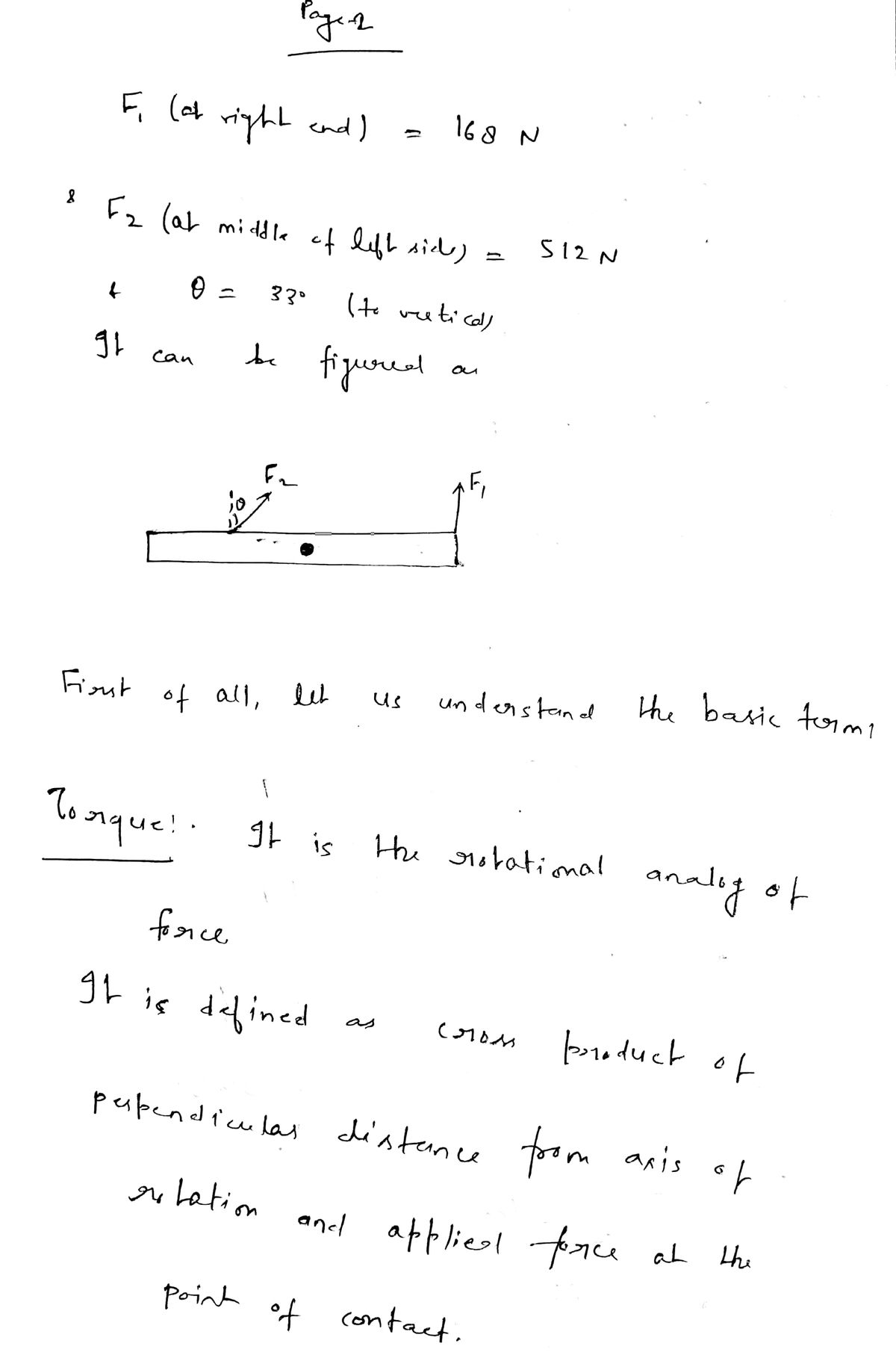
Consider a rod of total length 4 m that is free to pivot above its center. The linear mass density of the rod is given by λ(x) = 6 x4 (kg/m), where x is the distance from the center of the rod. The rod is in outer space, so you don't have to worry about any gravitational torques. There is a 168 N force that acts perpendicularly to the rod at its right end, and there is a 512 N force that acts halfway between the left end of the rod and its center. This force acts at an angle of 33 degrees to the vertical. This scenario is shown below:

Consider a rod of total length 4 m that is free to pivot above its center. The linear mass density of the rod is given by λ(x) = 6 x4 (kg/m), where x is the distance from the center of the rod. The rod is in outer space, so you don't have to worry about any gravitational torques. There is a 168 N force that acts perpendicularly to the rod at its right end, and there is a 512 N force that acts halfway between the left end of the rod and its center. This force acts at an angle of 33 degrees to the vertical. This scenario is shown below:

Similar questions

At an amusement park there is a ride in which cylindrically shaped chambers spin around a central axis. People sit in seats facing the axis, their backs against the outer wall. At one instant the outer wall moves at a speed of 2.72 m/s, and an 82.0-kg person feels a 276-N force pressing against his back. What is the radius of a chamber?
In 2014, the Rosetta space probe reached the comet Churyumov– Gerasimenko. Although the comet’s core is actually far from spherical, in this problem we’ll model it as a sphere with a mass of 1.0 x 1013 kg and a radius of 1.6 km. If a rock were dropped from a height of 1.0 m above the comet’s surface, how long would it take to hit the surface?
An aluminum rod is suspended by two wires, as shown in the figure below. The mass of the rod is 25.0 kg. Assume the rod has a uniform density. This means the gravitational force can be accurately modeled acting at the center of the rod.
A person is pushing a fully loaded 24.55 kg wheelbarrow at constant velocity along a plank that makes an angle a = 43.0° with the horizontal. The load is distributed such that the center of mass of the wheelbarrow is exactly halfway along its L. What is the magnitude of the total force F the person must apply so that the wheelbarrow is parallel to that plank? You may neglect the radius of the wheel in your analysis. The gravitational acceleration is g = 9.81 m/s². F = N
You are in a carnival ride that consists of a circular room that spins around its center. You stand against the wall at the edge of the room. The room spins at a constant rate of one revolution every 5 seconds, and the room has a radius of 5 m. Your mass is 70 kg. After the room reaches it final speed, the floor drops out from beneath you, yet you remain stuck to the wall. What is the magnitude of the normal force exerted on you by the wall, and at what rate (power) does the normal force perform work on you? (Please explain the power that the normal force does work in detail.)
Problem 2: A physical pendulum consists of a disk of radius R and mass 2m fixed at the end of a rod of mass 3m and length 4R as shown in the figure below. Please express your answers in terms of the given quantities and fundamental constants. 3m 4R R 2m a. Determine an expression for the position of the center of mass of the apparatus (relative to the upper end of the rod). Answer 2a:
The attached drawing shows two identical systems of objects, each consists of the same three small balls connected by massless rods. In both systems the axis is perpendicular to the page but it is located at different places as shown. The same magnitude of Force is applied to the same ball as indicated in the attached drawing. The masses of the balls are m1 = 9.5 kg; m2 = 6.2 kg; m3 = 7.3 kg. The magnitude of the force = 444N (a) For each of the two systems determine the moment of Inertia about the given axis of rotation (b) Calculate the torque, magnitude and direction, acting on each system (c) Both systems start from rest and the direction of the force moves with the system and always points along the 4.00 meter rod. What is the angular velocity of each system after 5.03 seconds
The drawing shows two identical systems of objects; each consists of the same three small balls connected by massless rods. In both systems the axis is perpendicular to the page, but it is located at a different place, as shown. The same force of magnitude F is applied to the same ball in each system (see the drawing). The masses of the balls are m1 = 9.0 kg, m2 = 6.1 kg, and m3 = 7.9 kg. The magnitude of the force is F = 441 N. (a) For each of the two systems, determine the moment of inertia about the given axis of rotation. (b) Calculate the torque (magnitude and direction) acting on each system. (c) Both systems start from rest, and the direction of the force moves with the system and always points along the 4.00-m rod. What is the angular velocity of each system after 5.35 s?
A meteoroid is moving towards a planet. It has mass m = 0.54×109 kg and speed v1 = 4.7×107 m/s at distance R1 = 1.6×107 m from the center of the planet. The radius of the planet is R = 0.78×107 m. The mass of the planet is M = 5.6×1025kg. There is no air around the planet. a)Enter an expression for the total energy E of the meteoroid at R, the surface of the planet, in terms of defined quantities and v, the meteoroid’s speed when it reaches the planet’s surface. Select from the variables below to write your expression. Note that all variables may not be required.α, β, θ, d, g, G, h, m, M, P, R, R1, t, v, v1 b)Enter an expression for v, the meteoroid’s speed at the planet’s surface, in terms of G, M, v1, R1, and R. c)Calculate the value of v in meters per second.
On a part-time job, you are asked to bring a cylindrical iron rod of density 7800 kg/m^3, length 89.2 cm and diameter 2.45 cm from a storage room to a machinist. Calculate the weight of the rod, w. Assume the free-fall acceleration is g = 9.80 m/s^2. Express you answer in N.
Problem 1: The figure shows a small sphere of mass m a distance D from the edge of a uniform rod of length L and mass M placed perpendicularly to the rod. The left edge of the rod is placed at the origin of an xy coordinate system. The x-direction points to the right, and the y-direction points up in the figure shown.The rod has a mass of 6.1 kg and the small sphere's mass is half the mass of the rod. The distance D = 1.4 m and the rod has a length of 1.4 m. What is the magnitude of the gravitational force, in newtons, of the ball?
A pulley has a negligible mass (that means, the radius is not relevant). It is supported with a pin at the center (and is free to rotate). A rope goes over the pulley. Block A, which has a mass of 5.723 kg is connected to one side of the rope. On the other side, Block B, with a mass of 12.602 kg is connected. The system is released from rest. What is the speed of block B, after B has traveled 0.716 m? Please enter a positive value in m/s (but without units) regardless of the direction of the motion of B