Homework Help is Here – Start Your Trial Now!
Math
Advanced Math
) Compute the value of the following improper integral. If it converges, enter its value. Enter infinity if it diverges to ∞, and -infinity if it diverges to -∞. Otherwise, enter diverges. [₁0⁰ 3 dx x² + 1 Does the series ∞ n=1 3 n² + 1 converge or diverge? ? >

) Compute the value of the following improper integral. If it converges, enter its value. Enter infinity if it diverges to ∞, and -infinity if it diverges to -∞. Otherwise, enter diverges. [₁0⁰ 3 dx x² + 1 Does the series ∞ n=1 3 n² + 1 converge or diverge? ? >

Advanced Engineering Mathematics
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
See similar textbooks
icon
Related questions
Question
) Compute the value of the following improper integral. If it converges, enter its value. Enter infinity if it diverges to ∞, and -infinity if it diverges to -∞. Otherwise, enter diverges. ∞ 1.₁ 3 dx x² + 1 = Does the series ∞ n=1 3 n² +1 converge or diverge? ?
Transcribed Image Text:) Compute the value of the following improper integral. If it converges, enter its value. Enter infinity if it diverges to ∞, and -infinity if it diverges to -∞. Otherwise, enter diverges. ∞ 1.₁ 3 dx x² + 1 = Does the series ∞ n=1 3 n² +1 converge or diverge? ?
i ) Compute the value of the following improper integral. If it converges, enter its value. Enter infinity if it diverges to ∞, and -infinity if it diverges to -0. Otherwise, enter diverges. [ 8x²e-³ dx = ∞ Does the series 8n² e-n²³ converge or diverge? ? n=1 >
Transcribed Image Text:i ) Compute the value of the following improper integral. If it converges, enter its value. Enter infinity if it diverges to ∞, and -infinity if it diverges to -0. Otherwise, enter diverges. [ 8x²e-³ dx = ∞ Does the series 8n² e-n²³ converge or diverge? ? n=1 >
Expert Solution
steps

Step by step

Solved in 2 steps with 1 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question

PLEASE REDO THIS

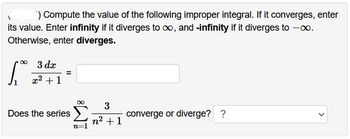
) Compute the value of the following improper integral. If it converges, enter its value. Enter infinity if it diverges to ∞, and -infinity if it diverges to -∞. Otherwise, enter diverges. ∞ 1.₁ 3 dx x² + 1 = Does the series ∞ n=1 3 n² +1 converge or diverge? ?
Transcribed Image Text:) Compute the value of the following improper integral. If it converges, enter its value. Enter infinity if it diverges to ∞, and -infinity if it diverges to -∞. Otherwise, enter diverges. ∞ 1.₁ 3 dx x² + 1 = Does the series ∞ n=1 3 n² +1 converge or diverge? ?
Solution
Bartleby Expert
SEE SOLUTION
Recommended textbooks for you
Advanced Engineering Mathematics
Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education
Introductory Mathematics for Engineering Applicat…
Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY
Mathematics For Machine Technology
Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,
Basic Technical Mathematics
Basic Technical Mathematics
Advanced Math
ISBN:
9780134437705
Author:
Washington
Publisher:
PEARSON
Topology
Topology
Advanced Math
ISBN:
9780134689517
Author:
Munkres, James R.
Publisher:
Pearson,
SEE MORE TEXTBOOKS