Compute the product AB by the definition of the product of matrices, where Ab₁ and Ab₂ are computed separately, and by the row-column rule for computing AB. A = -2 2 2 5 6-3 B= 5-2 -1 4
Compute the product AB by the definition of the product of matrices, where Ab₁ and Ab₂ are computed separately, and by the row-column rule for computing AB. A = -2 2 2 5 6-3 B= 5-2 -1 4
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
Hello there! Can you help me solve a problem with one of the subparts? Thanks!
![**Matrix Multiplication Explanation**
In this section, we'll compute the product of matrices \( AB \) using the definition of matrix multiplication. We will compute the product separately for \( Ab_1 \) and \( Ab_2 \), and then demonstrate the row-column rule for computing \( AB \).
**Matrix Definitions:**
\[
A =
\begin{bmatrix}
-2 & 2 \\
2 & 5 \\
6 & -3
\end{bmatrix}
\]
\[
B =
\begin{bmatrix}
5 & -2 \\
-1 & 4
\end{bmatrix}
\]
**Procedure to Compute AB:**
1. **Identify Columns of B:**
- \( b_1 = \begin{bmatrix} 5 \\ -1 \end{bmatrix} \)
- \( b_2 = \begin{bmatrix} -2 \\ 4 \end{bmatrix} \)
2. **Compute Ab1:**
- Multiply matrix \( A \) with the column \( b_1 \).
- Result: \( Ab_1 \)
3. **Compute Ab2:**
- Multiply matrix \( A \) with the column \( b_2 \).
- Result: \( Ab_2 \)
4. **Construct the Product Matrix AB:**
- Combine results \( Ab_1 \) and \( Ab_2 \) into matrix \( AB \) using the row-column multiplication rule.
**Explanation of Matrix Multiplication:**
- Each element in the product matrix \( AB \) is computed as the dot product of the corresponding row of \( A \) with the column of \( B \).
By following these steps, you can achieve the matrix product \( AB \).
Note: Detailed computation steps and results for \( Ab_1 \) and \( Ab_2 \) should be calculated to determine the final product matrix \( AB \).](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fe00cebfb-aec4-474d-8979-79a2d105b819%2Fc8e72c50-014d-4963-bda6-2a572ae7df6f%2F6fq3jno_processed.png&w=3840&q=75)
Transcribed Image Text:**Matrix Multiplication Explanation**
In this section, we'll compute the product of matrices \( AB \) using the definition of matrix multiplication. We will compute the product separately for \( Ab_1 \) and \( Ab_2 \), and then demonstrate the row-column rule for computing \( AB \).
**Matrix Definitions:**
\[
A =
\begin{bmatrix}
-2 & 2 \\
2 & 5 \\
6 & -3
\end{bmatrix}
\]
\[
B =
\begin{bmatrix}
5 & -2 \\
-1 & 4
\end{bmatrix}
\]
**Procedure to Compute AB:**
1. **Identify Columns of B:**
- \( b_1 = \begin{bmatrix} 5 \\ -1 \end{bmatrix} \)
- \( b_2 = \begin{bmatrix} -2 \\ 4 \end{bmatrix} \)
2. **Compute Ab1:**
- Multiply matrix \( A \) with the column \( b_1 \).
- Result: \( Ab_1 \)
3. **Compute Ab2:**
- Multiply matrix \( A \) with the column \( b_2 \).
- Result: \( Ab_2 \)
4. **Construct the Product Matrix AB:**
- Combine results \( Ab_1 \) and \( Ab_2 \) into matrix \( AB \) using the row-column multiplication rule.
**Explanation of Matrix Multiplication:**
- Each element in the product matrix \( AB \) is computed as the dot product of the corresponding row of \( A \) with the column of \( B \).
By following these steps, you can achieve the matrix product \( AB \).
Note: Detailed computation steps and results for \( Ab_1 \) and \( Ab_2 \) should be calculated to determine the final product matrix \( AB \).

Transcribed Image Text:**Determine the product AB.**
AB = ☐
*Use integers or decimals for any numbers in the expression.*
Expert Solution
Step 1: Given data
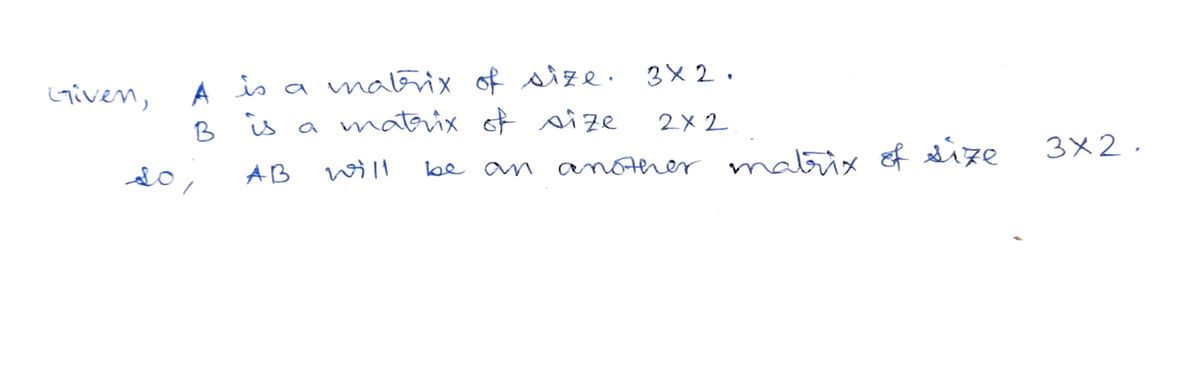
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

