Homework Help is Here – Start Your Trial Now!
Math
Advanced Math
Compare and contrast reflections over the x-axis and y-axis. Generalize your observations

Compare and contrast reflections over the x-axis and y-axis. Generalize your observations

Advanced Engineering Mathematics
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
See similar textbooks
icon
Related questions
Question
Compare and contrast reflections over the x-axis and y-axis. Generalize your observations. How does the function behave relative to the location of the negative coefficient? y = − x² vs y = (-x)² or y = √−r vs y VT
Transcribed Image Text:Compare and contrast reflections over the x-axis and y-axis. Generalize your observations. How does the function behave relative to the location of the negative coefficient? y = − x² vs y = (-x)² or y = √−r vs y VT
Expert Solution
Step 1

# As per the guidelines we are entitled to solve one question at a time, please resubmit the other question if you wish to get it answered.

Consider a point (x,y) if the reflection is over x-axis, the x coordinate will remain same and the y co-ordinate will be the additive inverse of the original coordinate.

Therefore, the reflection over x- axis will make the point (x,-y).

It basically will change the side of point over the axis, that is if the point is below the x- axis after reflection it will be up the x- axis, and vice- versa.

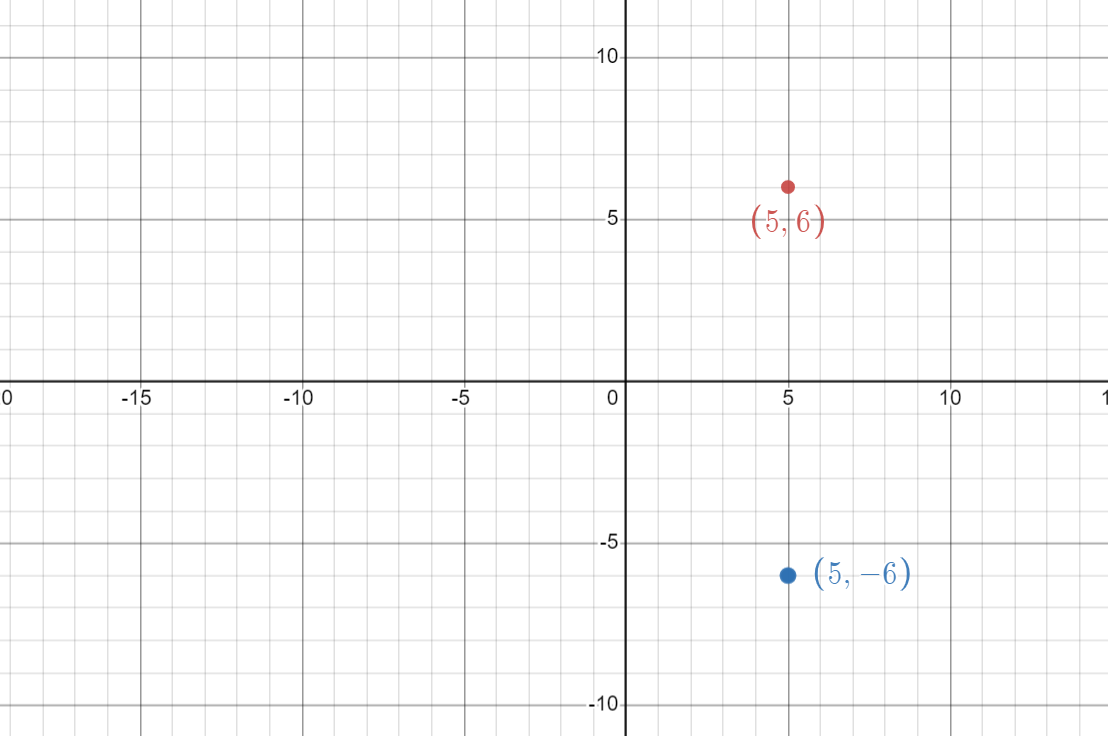
Advanced Math homework question answer, step 1, image 1

The original point (5,6) is above the x-axis, after reflection over x- axis it is below the x-axis.

steps

Step by step

Solved in 2 steps with 2 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Recommended textbooks for you
Advanced Engineering Mathematics
Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education
Introductory Mathematics for Engineering Applicat…
Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY
Mathematics For Machine Technology
Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,
Basic Technical Mathematics
Basic Technical Mathematics
Advanced Math
ISBN:
9780134437705
Author:
Washington
Publisher:
PEARSON
Topology
Topology
Advanced Math
ISBN:
9780134689517
Author:
Munkres, James R.
Publisher:
Pearson,
SEE MORE TEXTBOOKS