**Problem Statement** Define the function: \[ h(x) = \frac{f(x) \cdot g(x) - 10}{g(x)} \] Now suppose the following values: - \( f(2) = 7 \) - \( f'(2) = -5 \) - \( g(2) = 3 \) - \( g'(2) = -4 \) Find \( h'(2) \). **Solution Explanation** To solve for \( h'(2) \), you would typically apply the quotient rule for derivatives to the function \( h(x) \). The quotient rule states that for a function \( \frac{u(x)}{v(x)} \), the derivative is given by: \[ \left( \frac{u}{v} \right)' = \frac{u'v - uv'}{v^2} \] Here: - \( u(x) = f(x) \cdot g(x) - 10 \) - \( v(x) = g(x) \) You will need to find \( u'(x) \) and \( v'(x) \), and then substitute the given values to find \( h'(2) \).
**Problem Statement** Define the function: \[ h(x) = \frac{f(x) \cdot g(x) - 10}{g(x)} \] Now suppose the following values: - \( f(2) = 7 \) - \( f'(2) = -5 \) - \( g(2) = 3 \) - \( g'(2) = -4 \) Find \( h'(2) \). **Solution Explanation** To solve for \( h'(2) \), you would typically apply the quotient rule for derivatives to the function \( h(x) \). The quotient rule states that for a function \( \frac{u(x)}{v(x)} \), the derivative is given by: \[ \left( \frac{u}{v} \right)' = \frac{u'v - uv'}{v^2} \] Here: - \( u(x) = f(x) \cdot g(x) - 10 \) - \( v(x) = g(x) \) You will need to find \( u'(x) \) and \( v'(x) \), and then substitute the given values to find \( h'(2) \).
Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
Related questions
Question
![**Problem Statement**
Define the function:
\[ h(x) = \frac{f(x) \cdot g(x) - 10}{g(x)} \]
Now suppose the following values:
- \( f(2) = 7 \)
- \( f'(2) = -5 \)
- \( g(2) = 3 \)
- \( g'(2) = -4 \)
Find \( h'(2) \).
**Solution Explanation**
To solve for \( h'(2) \), you would typically apply the quotient rule for derivatives to the function \( h(x) \). The quotient rule states that for a function \( \frac{u(x)}{v(x)} \), the derivative is given by:
\[ \left( \frac{u}{v} \right)' = \frac{u'v - uv'}{v^2} \]
Here:
- \( u(x) = f(x) \cdot g(x) - 10 \)
- \( v(x) = g(x) \)
You will need to find \( u'(x) \) and \( v'(x) \), and then substitute the given values to find \( h'(2) \).](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F1bdbbc13-ac05-4028-8ad3-717acbe8710a%2F9ff601b2-d17d-463c-8b5b-d5311b6c6a29%2Fknklbaq.jpeg&w=3840&q=75)
Transcribed Image Text:**Problem Statement**
Define the function:
\[ h(x) = \frac{f(x) \cdot g(x) - 10}{g(x)} \]
Now suppose the following values:
- \( f(2) = 7 \)
- \( f'(2) = -5 \)
- \( g(2) = 3 \)
- \( g'(2) = -4 \)
Find \( h'(2) \).
**Solution Explanation**
To solve for \( h'(2) \), you would typically apply the quotient rule for derivatives to the function \( h(x) \). The quotient rule states that for a function \( \frac{u(x)}{v(x)} \), the derivative is given by:
\[ \left( \frac{u}{v} \right)' = \frac{u'v - uv'}{v^2} \]
Here:
- \( u(x) = f(x) \cdot g(x) - 10 \)
- \( v(x) = g(x) \)
You will need to find \( u'(x) \) and \( v'(x) \), and then substitute the given values to find \( h'(2) \).
Expert Solution
Step 1
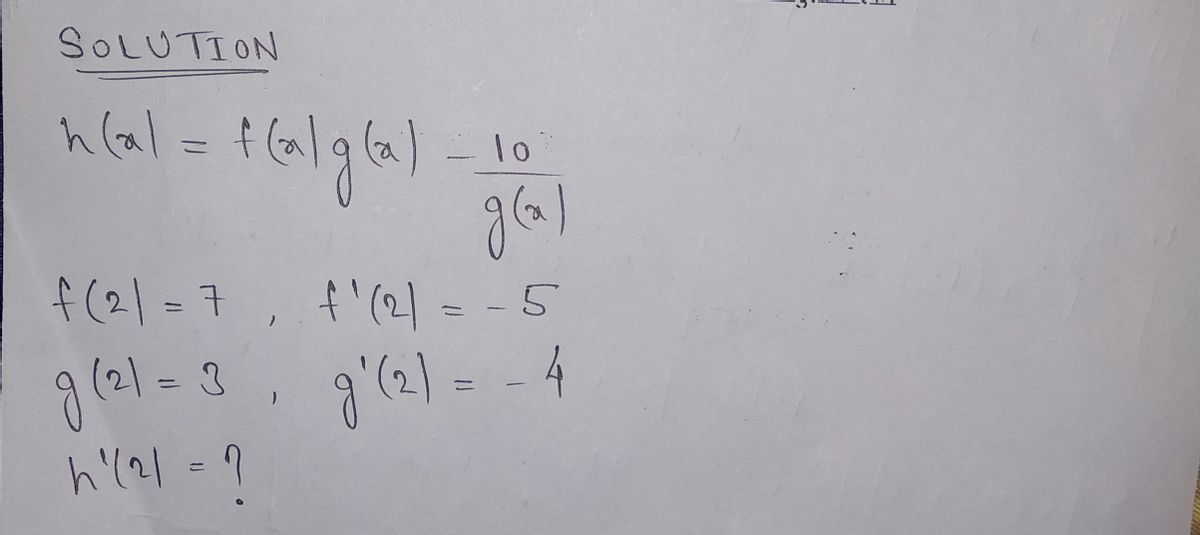
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning