We have solved first three parts of the questions, if you want answer to other parts, resubmit the question with that part.
Let the critical point of f(x) be c.
To find the critical points of f(x), we need to differentiate f(x), for at critical point f(x) is either undefined or zero.
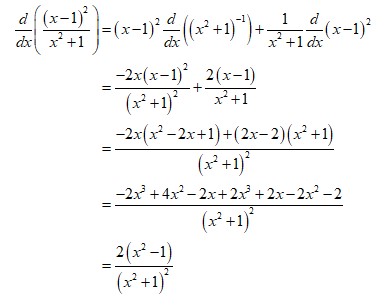
Set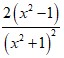 
equal to zero, it will not be undefined for any value of x.
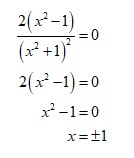
Thus, the critical points of the function f(x) are 1,-1.
Draw the graph of the function f '(x).
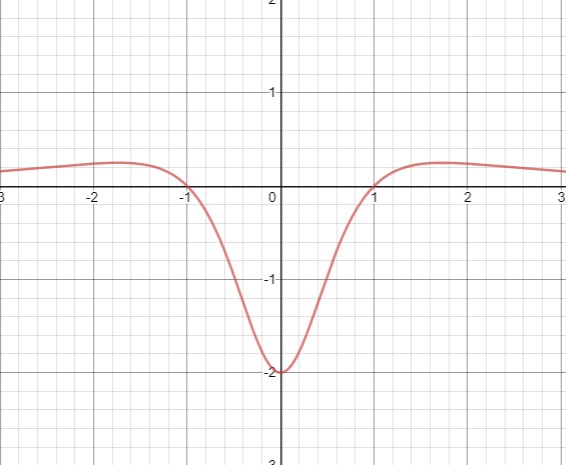
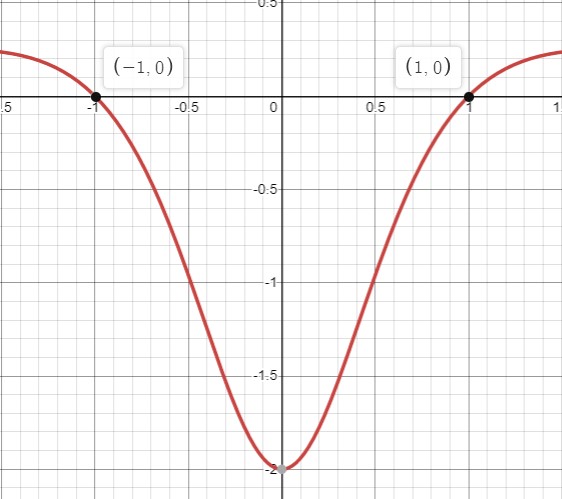
Since the function f(x) is increasing when f '(x) > 0 and decreasing when f '(x) < 0, thus, the function f (x) is increasing when x lies in the interval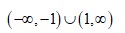 
and decreasing when x lies in the interval 
.
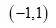To find where the function is concave up and concave down, we need to find the differential of the function f '(x), for the function f(x) is concave up when f ''(x) > 0 and concave down when f ''(x) < 0.
Step by step
Solved in 7 steps with 11 images
