(-3) = f(3) = 0 %3D f'(0) = f'(2) = 0 f'(x) > 0 for x < 0 (x) > 0 for O < x < 2 f'(x) < 0 for x > 2 f"(x) < 0 for x < 0 or x > 1 f"(x) > 0 for 0 < x < 1

The function f possesses below characteristics,
- f(-3)=f(3)=0
- f'(0)=f'(2)=0
- f'(x)>0 , for x < 0
- f'(x)>0 , for 0< x < 2
- f'(x) < 0 for x > 2
- f"(x)<0 for x<0 or x>1
- f"(x)>0 for 0< x < 1
If f(x) = 0 , then values of x are the zeros of function.
Here, f(-3) = f(3) = 0
=> -3 and 3 are zeros of the function f.
So curve passes through the points (-3,0) and (3,0) on graph of function f.
The critical points are the points which satisfies the equation f'(x) = 0.
Here, f'(0)=f'(2)=0
=> 0 and 2 are the critical points of function f .
That is, there is nodes at points 0 and 2.
If f'(x) > 0 in an interval then function f is increasing in that respective interval.
Here, f'(x)>0 , for x < 0 and f'(x)>0 , for 0< x < 2.
=> Function f is increasing on interval 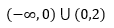
If f'(x) < 0 on an interval then function f is decreasing on that respective interval.
Here, f'(x) < 0 for x > 2.
=> Function f is decreasing on interval 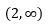 .
.
By second derivative test,
If f"(x)<0 for some interval then function f is concave down in that respective interval whose end points are the inflection points.
Here, f"(x)<0 for x<0 or x>1.
=> Function f is concave down for intervals  .
.
If f"(x)>0 for some interval then function f is concave up in that respective interval whose end points are the inflection points.
Here, f"(x)>0 for 0< x < 1 .
=> Function is concave up on interval 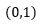 .
.
Step by step
Solved in 3 steps with 5 images









