c. Using the original formulas for T, x, and y in the problem statement, calculate all of the derivatives in Equation (10.5.2) (with Ta and Ty in terms of x and y, and r' and y' in terms of t), and hence write the right-hand side of Equation (10.5.2) in terms of x, y, and t.
c. Using the original formulas for T, x, and y in the problem statement, calculate all of the derivatives in Equation (10.5.2) (with Ta and Ty in terms of x and y, and r' and y' in terms of t), and hence write the right-hand side of Equation (10.5.2) in terms of x, y, and t.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
Please help with c. A is attached for reference.

Transcribed Image Text:CHAPTER 10. DERIVATIVES OF MULTIVARIABLE FUNCTIONS 73
10.5 The Chain Rule
Preview Activity 10.5.1 Suppose you are driving around in the xy-plane in
such a way that your position r(t) at time t is given by function
r(t) = (x(t), y(t)) = (2 − t², t³ + 1).
The path taken is shown on the left of Figure 10.5.1.
21
3-
2-
1
Y
by
1
2
X
3
I
Figure 10.5.1 Left: Your position in the plane. Right: The corresponding
temperature.
Suppose, furthermore, that the temperature at a point in the plane is given
Y
T(x, y) 10-1²-²,
=
and note that the surface generated by T is shown on the right of Figure 10.5.1.
Therefore, as time passes, your position (x(t), y(t)) changes, and, as your po-
sition changes, the temperature T(x, y) also changes.
a. The position function r provides a parametrization x = x(t) and y = = y(t)
of the position at time t. By substituting ä(t) for x and y(t) for y in the
formula for T, we can write T = T(x(t), y(t)) as a function of t. Make
these substitutions to write T as a function of t and then use the Chain
Rule from single variable calculus to find d. (Do not do any algebra to
simplify the derivative, either before taking the derivative, nor after.)
dt

Transcribed Image Text:ATT₂Ax+ TyAy.
The Chain Rule tells us about the instantaneous rate of change of T, and
this can be found as
ΔΤ
lim
= lim
At→0 At At →0
(10.5.1)
Use equation (10.5.1) to explain why the instantaneous rate of change of
T that results from a change in t is
dT
dt
TzAx+TyAy
At
ƏT dx
Əx dt
ᏭᎢ dy
+
dy dt
(10.5.2)
c. Using the original formulas for T, x, and y in the problem statement,
calculate all of the derivatives in Equation (10.5.2) (with T₂ and Ty in
terms of x and y, and x' and y' in terms of t), and hence write the
right-hand side of Equation (10.5.2) in terms of x, y, and t.
Expert Solution
Step 1
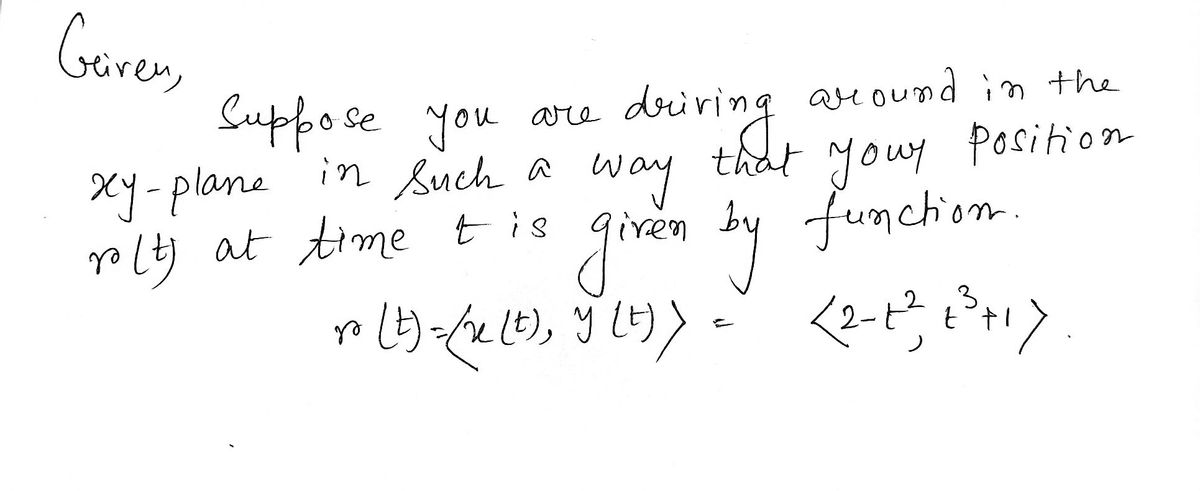
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

