(c) The motion of a particle in a plane is governed by the Lagrangian 1 1 L = ; (x² + ÿ³) + ¿(vi – wý). (i) Obtain the equations of motion (simplify if possible). Is the force acting on the particle conservative? (ii) Verify that = Rcos t, y = Rsin t, is a solution of the equations of motion (here R is a constant). (iii) What is the general form of the solutions? Hint: The solution from part (ii) has one arbitrary constant R. The general solution includes four arbitrary constants.
(c) The motion of a particle in a plane is governed by the Lagrangian 1 1 L = ; (x² + ÿ³) + ¿(vi – wý). (i) Obtain the equations of motion (simplify if possible). Is the force acting on the particle conservative? (ii) Verify that = Rcos t, y = Rsin t, is a solution of the equations of motion (here R is a constant). (iii) What is the general form of the solutions? Hint: The solution from part (ii) has one arbitrary constant R. The general solution includes four arbitrary constants.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
Repost for part iii

Transcribed Image Text:(c) The motion of a particle in a plane is governed by the Lagrangian
L = } (4² + o*) + (ut – rý).
1
1
2
2
(i) Obtain the equations of motion (simplify if possible). Is the force acting on the
particle conservative?
(ii) Verify that
x = Rcos t,
y = Rsin t,
is a solution of the equations of motion (here R is a constant).
(iii) What is the general form of the solutions?
Hint: The solution from part (ii) has one arbitrary constant R. The general
solution includes four arbitrary constants.
Expert Solution
Step 1
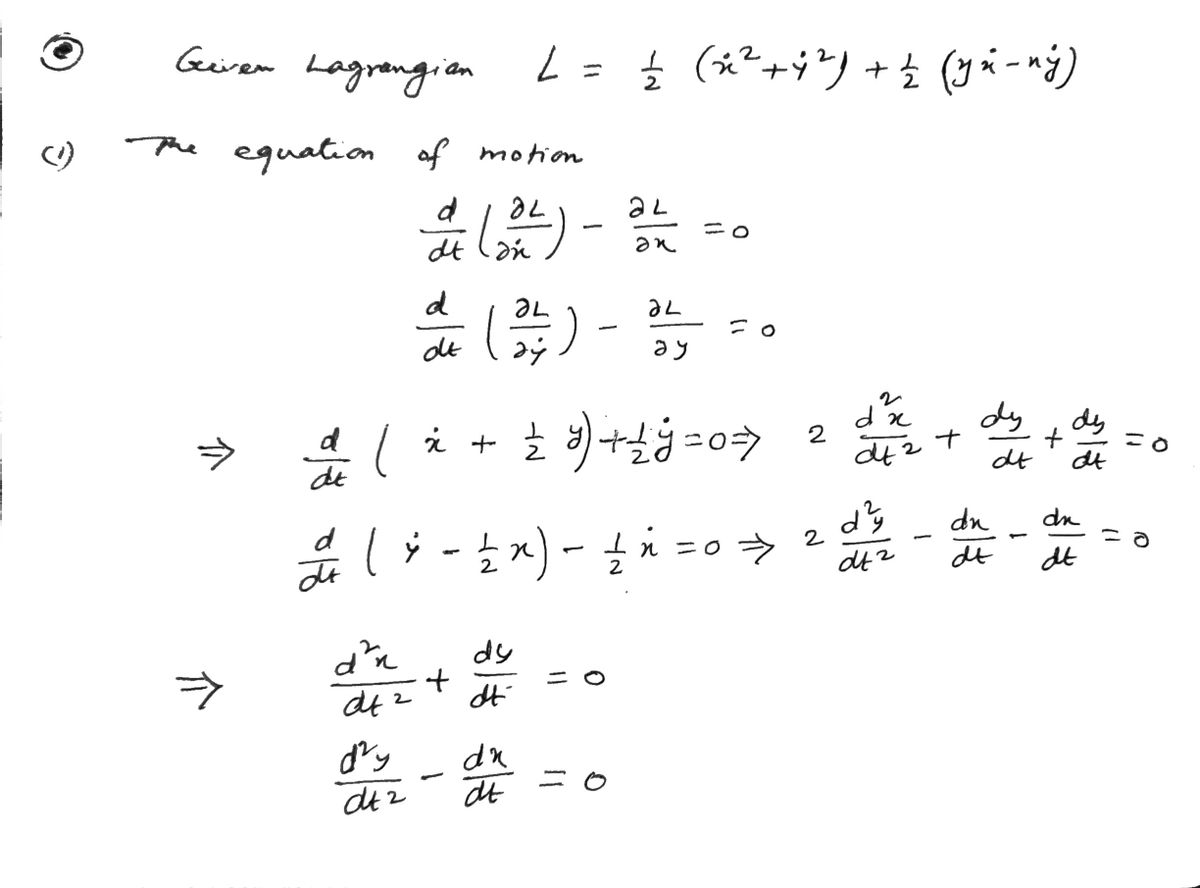
Step by step
Solved in 4 steps with 4 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

