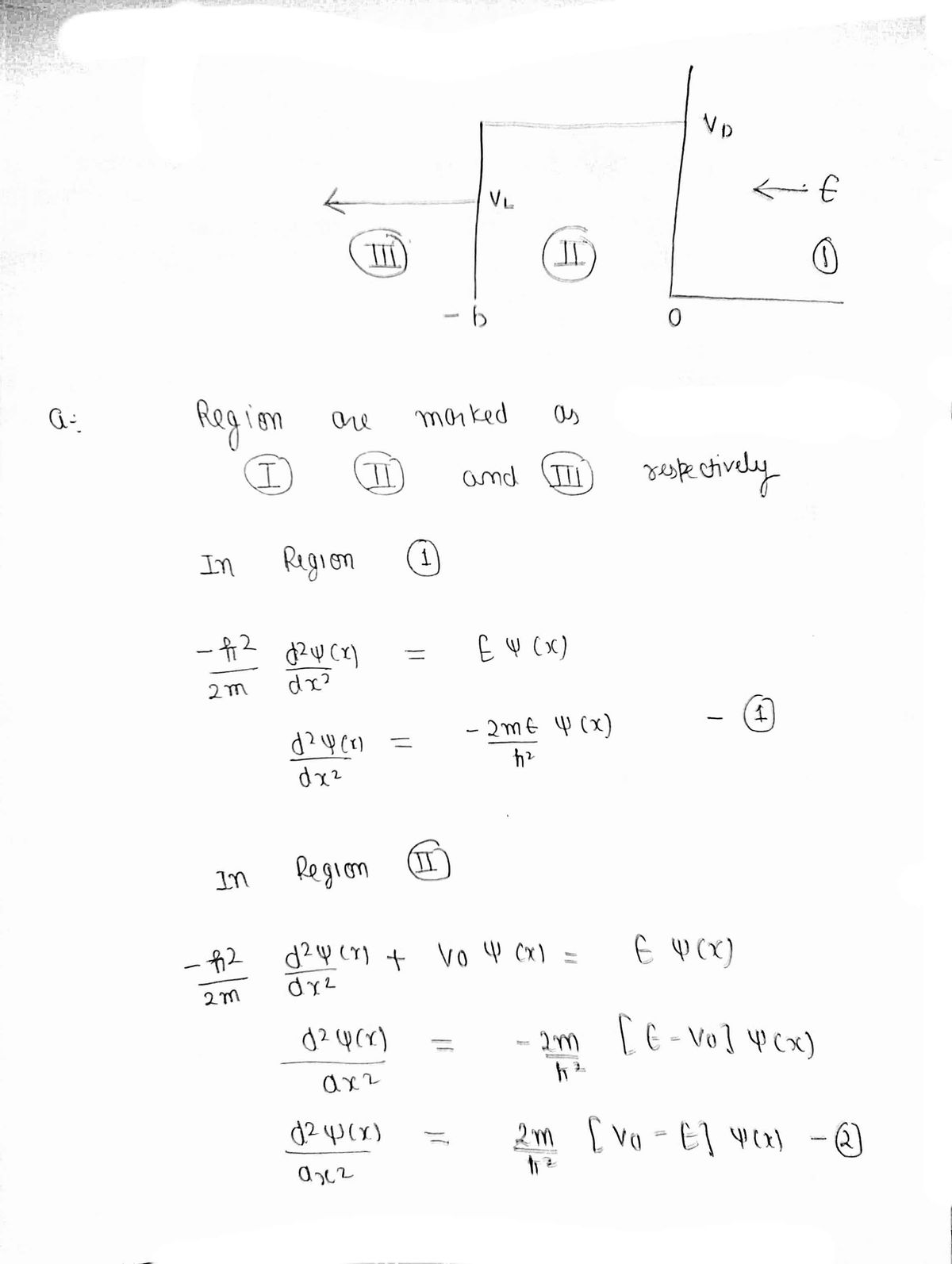
Background: In quantum mechanics, one can understand a lot about the wave nature of particles by solving simple one-dimensional scattering problems. A common problem is phrased by considering an incident beam of particles onto some region of space where differences in potential energy is experienced by the particles. These regions are modeled as piecewise constant potential regions. For example, consider the picture to the right. Question: (a) Write down three different time independent Schrodinger equations for each region. (b) Write down the form of the solution to each of these equations. (c) Write down what the boundary conditions are at each interface. Do not attempt to solve these equations. V(x), E V, x = -b x =0
Background: In quantum mechanics, one can understand a lot about the wave nature of particles by solving simple one-dimensional scattering problems. A common problem is phrased by considering an incident beam of particles onto some region of space where differences in potential energy is experienced by the particles. These regions are modeled as piecewise constant potential regions. For example, consider the picture to the right. Question: (a) Write down three different time independent Schrodinger equations for each region. (b) Write down the form of the solution to each of these equations. (c) Write down what the boundary conditions are at each interface. Do not attempt to solve these equations. V(x), E V, x = -b x =0
Related questions
Question

Transcribed Image Text:**Background:** In quantum mechanics, one can understand a lot about the wave nature of particles by solving simple one-dimensional scattering problems. A common problem is phrased by considering an incident beam of particles onto some region of space where differences in potential energy is experienced by the particles. These regions are modeled as piecewise constant potential regions. For example, consider the picture to the right.
**Question:**
(a) Write down three different time-independent Schrödinger equations for each region.
(b) Write down the form of the solution to each of these equations.
(c) Write down what the boundary conditions are at each interface. Do not attempt to solve these equations.
**Graph Description:**
The diagram shows a potential energy graph with three distinct regions along the x-axis:
1. **Region I (x = -b):** The potential energy \( V(x) = V_L \), where the potential is constant and lower than \( V_b \).
2. **Region II (0 < x < -b):** The potential is at a different constant level, \( V(x) = V_b \).
3. **Region III (x = 0):** Potential continues to be \( V_b \) and the direction of particle motion is indicated by an arrow \( E \) pointing to the right.
Expert Solution
Step 1
Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 3 images
