An "infinite" solenoid has 968 turns/m and circular cross section of radius 15.3 m. A small circular coil (806 turns, radius 75.6 mm, resistance 3.07 Q, is placed inside the solenoid so its axis is parallel to the axis of the solenoid. This time, the solenoid is connected to an AC source. At t = 0, the power is turned on, and the current in the solenoid is given by: Isol = 41.9cos(54t), where t is in seconds and is in A. Find Irms, the rms current induced in the small coil, in A. Give the answer as a positive number.
An "infinite" solenoid has 968 turns/m and circular cross section of radius 15.3 m. A small circular coil (806 turns, radius 75.6 mm, resistance 3.07 Q, is placed inside the solenoid so its axis is parallel to the axis of the solenoid. This time, the solenoid is connected to an AC source. At t = 0, the power is turned on, and the current in the solenoid is given by: Isol = 41.9cos(54t), where t is in seconds and is in A. Find Irms, the rms current induced in the small coil, in A. Give the answer as a positive number.
Related questions
Question
Question in the attachments
Transcribed Image Text:An "infinite" solenoid has 968 turns/m and circular cross section of radius 15.3 m. A small circular coil (806 turns,
radius 75.6 mm, resistance 3.07 Q, is placed inside the solenoid so its axis is parallel to the axis of the solenoid.
This time, the solenoid is connected to an AC source. At t = 0, the power is turned on, and the current in the solenoid
is given by:
Isol = 41.9cos(54t), where t is in seconds and / is in A.
%3D
Find Irms, the rms current induced in the small coil, in A. Give the answer as a positive number.
Expert Solution
Concept
According to Faraday's law of electromagnetic induction
The induced emf through a coil is given by
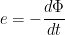
Where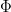 
= Magnetic flux through coil, t = time, e = induced emf
The magnetic flux through the coil is given by
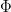= NB.A
Where N = number of turns of the coil, B = Magnetic field through the coil, A = Area of the coil in the magnetic field.
The magnetic field (inside solenoid) due to the infinite solenoid is given by
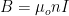
Where n = number of turns of solenoid per unit length, I = Current in the solenoid,
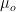= Magnetic permeability of free space = 4π × 10- 7 T.m.A- 1
Step by step
Solved in 3 steps with 11 images
