An engineer is measuring a quantity 0. It is assumed that there is a random error in each measurement, so the engineer will take n measurements and report the average of the measurements as the estimated value of 0. Here, n is assumed to be large enough so that the central limit theorem applies. If X, is the value that is obtained in the ith measurement, we assume that X; = 0 + W, where W, is the error in the ith measurement. We assume that the W,'s are i.i.d. with EW, = 0 and Var(") = 4 units. The engineer reports the average of the measurements X, + X2+...+X, X = How many measurements does the engineer need to make until he is 90% sure that the final error is less than 0.25 units? In other words, what should the value of n be such that P(0 – 0.25 < X <0 + 0.25) 2 .90?

An engineer is measuring a quantity 0. It is assumed that there is a random error in each measurement, so the engineer will take n measurements and report the average of the measurements as the estimated value of 0. Here, n is assumed to be large enough so that the central limit theorem applies. If X, is the value that is obtained in the ith measurement, we assume that X; = 0 + W, where W, is the error in the ith measurement. We assume that the W,'s are i.i.d. with EW, = 0 and Var(") = 4 units. The engineer reports the average of the measurements X, + X2+...+X, X = How many measurements does the engineer need to make until he is 90% sure that the final error is less than 0.25 units? In other words, what should the value of n be such that P(0 – 0.25 < X <0 + 0.25) 2 .90?

MATLAB: An Introduction with Applications

6th Edition

ISBN:9781119256830

Author:Amos Gilat

Publisher:Amos Gilat

Chapter1: Starting With Matlab

Section: Chapter Questions

Problem 1P

See similar textbooks

Related questions

Q: A random process X(1) is defined as X(1) = A¸ cos(2#f,1) +A, sin(2¤f1) where A, and A, are…

A: Hello! As you have posted more than 3 sub parts, we are answering the first 3 sub-parts. In case…

Q: 2.suppose that x1,x2,...,xn be ar.s of size n from exponential dist. with parameter 0, find the MVBE…

A: Step 1:Problem StatementSuppose that x1,x2,...,xn are i.i.d. (independently and identically…

Q: If = 35, = 27, and s = 2, what is the associated zi value?

A: Given data,x=35μ=27s=2z=?

Q: i.i.d. Let X1,..., Xn Poisson(A) and let A = E, X; = Xn. Find the bias, stan- (a) dard error (SE),…

A: @solution:::

Q: Jim’s bookcase holds 4 geometry books, 1 calculus book, and 3 algebra books. Books are taken at…

A: Total number of books in the bookcase is 8 (4 +3+1) Number of books other day algebra book is 5…

Q: cle with a particular defect in its emission control system is taken to a succession of randomly…

Q: 8.4.1. Let X be N(0,0) and, in the notation of this section, let' = 4,0" = 9, %a = 0.10. Show that…

A: Given: The given distribution isN(0,θ)Let θ'=4 and θn=9αα=0.05ßß=0.10

Q: Q.4 a. b. C. X is uniform in [0,4] and Y= 4logel4/X) What is the pdf of Y? What is the mean of Y?…

A: Q4. Given that random variable is uniform in ,so it's probability density function is the…

Q: uppose X and Y are independent random variables. If the pdf of x is xe ",x ≥ 0 and the pdf of y is…

A: Solution

Q: 5. The voltage X across a 3 Ohms resistor is a uniform random variable with limits [0,4]. Given that…

A: Given that X is a uniform variable with limits [0, 4].Y=X2/3

Q: A small city is divided into four quadrants of 25 square kilometers each and has two fire trucks…

A: μA=∫A10-3dx×dy for A⊂-5, 5×-5, 5

Q: The following data are number of months in service of air conditioning units in airplanes before the…

A: The data values of the no. of months in service of air conditioning units in airplanes before the…

Q: i.i.d. Consider Y₁,..., Yn Bern(p). Consider the following estimator: p = n Y with probability n-1…

A: Given information: p^=Y¯ with probability n-1nn with probability 1n

Q: .8.3 Suppose X is uniformly distributed over the interval [0, 3], and Y = (X− 1)². Find the CDF,…

Q: 103 and o = 5. Determine the following Assume X is a normally distributed continuous variable with u…

A: Given Information:Mean, μ=103Standard Deviation, σ=5To find out Px≤88

Q: The current in a semiconductor diode is often measured by the Shockley equation I = 10(eav 1) where…

A: Step 1:Step 2:

Q: aving obtained a random sample from a population, you want to use a χ-squared test for determine…

A: a) Given: Number of intervals = 6 Each interval has equal probability = 16…

Q: How a single interpretation is possible for μ1 – μ2?

A: The parameter of interest is the difference in population means, μ1 - μ2. Where, μ1 and μ2 are the…

Q: Let X1, . . . , Xn, . . . ∼ iid Bern(θ). Consider the Bayes estimator under squared error loss with…

A: The Bayes estimator under squared error loss for the parameter given a uniform (0,1) prior is the…

Q: Suppose TE L(V) is normal. Prove that Im(T) = Im(T*). t: Show that Im(T) = Im(TT*). Problem 10 from…

Question

An engineer is measuring a quantity 0. It is assumed that there is a random error in
each measurement, so the engineer will take n measurements and report the average
of the measurements as the estimated value of 0. Here, n is assumed to be large
enough so that the central limit theorem applies. If X, is the value that is obtained in
the ith measurement, we assume that
X; = 0 + W,,
where W, is the error in the ith measurement. We assume that the W,'s are i.i.d. with
EW, = 0 and Var(") = 4 units. The engineer reports the average of the
measurements
X, + X2+..+X,
X =
How many measurements does the engineer need to make until he is 90% sure that
the final error is less than 0.25 units? In other words, what should the value of n be
such that
P(0 – 0.25 < X < 0 + 0.25) > .90?

Expert Solution

This question has been solved!

Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.

This is a popular solution!

SEE SOLUTION Check out a sample Q&A here

Step 1

VIEW

Step 2

VIEW

Step 3

VIEW

Trending now

This is a popular solution!

Step by step

Solved in 3 steps with 3 images

SEE SOLUTION Check out a sample Q&A here

Follow-up Questions

Read through expert solutions to related follow-up questions below.

Follow-up Question

can you explain ? thank you !

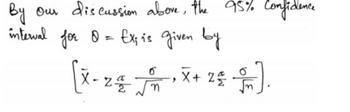
By our discussion above, the 95% Confidence
interval for 0 = Ex; is given by
6
(x - 2 € √ X + 25 ²5 ).
-
ท

Solution

by Bartleby Expert

SEE SOLUTION

Similar questions

Please show the full steps.
3. Let X1, and E- X; are independent. , Xn be iid with exponential distribution with mean 0. Show that (X1+X2)/ E=1 X;
Let {Xi} from i to n be IID from Bernoulli(p). Find the MQ estimator of p.
Kelvin’s bookcase holds 2 algebra books, 1 calculus book, and 4 geometry books. Books are taken at random from his bookcase, one after another and without replacement, until a geometry book is had, at which point no more books are taken. The random variable Y represents the total number of books taken during this experiment. Find Pr[ Y = 3 ].
Suppose that X1, X2, ..., Xn is a random sample with a probability law P(x) = {0x, 0 Where 8 is an unknown parameter. si x = 1,2,3, 4; otherwise A. Get an estimator of 0 by the method of the moments. B. Prove that the estimator is unbiased.
2.11 Let X have the standard normal pdf, fx(x) = (1/√√2π) e¯2²/² (a) Find EX² directly, and then by using the pdf of Y = X2 from Example 2.1.7 and calculating EY. (b) Find the pdf of Y = |X|, and find its mean and variance.
The mean of the random variable X is ux = 38 and the coefficient of variation is Vx = 0.37. Let Z be the standard form of X. If the result of an experiment is X = 4, what is the corresponding value of Z? QUESTION 8 If the cumulative distribution function for X is Fx(x) function, and it has to return an angle in radians, not degrees. 1 1 +tan (a*), what is P(0 < X < 1.20)? Note that tan 1 is the arctangent 2