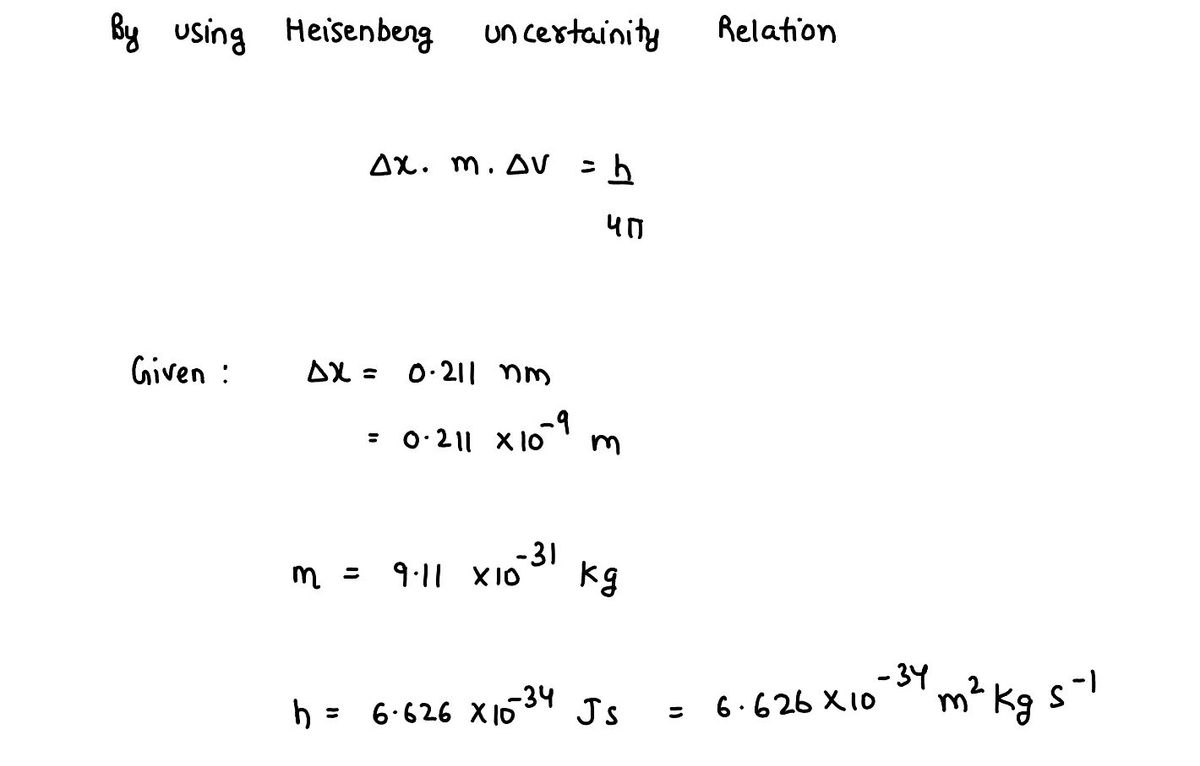
An electron is located within an interval of 0.211 nm in the north-south direction. What is the minimum uncertainty Au in the electron's velocity in that direction? The Heisenberg uncertainty relation is given different forms in different textbooks. Use the form employing > Av= m/s
An electron is located within an interval of 0.211 nm in the north-south direction. What is the minimum uncertainty Au in the electron's velocity in that direction? The Heisenberg uncertainty relation is given different forms in different textbooks. Use the form employing > Av= m/s
Chemistry
10th Edition
ISBN:9781305957404
Author:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCoste
Publisher:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCoste
Chapter1: Chemical Foundations
Section: Chapter Questions
Problem 1RQ: Define and explain the differences between the following terms. a. law and theory b. theory and...
Related questions
Concept explainers
Atomic Structure
The basic structure of an atom is defined as the component-level of atomic structure of an atom. Precisely speaking an atom consists of three major subatomic particles which are protons, neutrons, and electrons. Many theories have been stated for explaining the structure of an atom.
Shape of the D Orbital
Shapes of orbitals are an approximate representation of boundaries in space for finding electrons occupied in that respective orbital. D orbitals are known to have a clover leaf shape or dumbbell inside where electrons can be found.
Question
![### Understanding the Heisenberg Uncertainty Principle
**Problem Statement:**
An electron is located within an interval of 0.211 nm in the north-south direction. What is the minimum uncertainty (∆v) in the electron's velocity in that direction?
**Concept Explanation:**
The Heisenberg Uncertainty Principle is a fundamental theory in quantum mechanics that states that it is impossible to simultaneously know both the position and the velocity of a particle with absolute certainty. This principle is expressed in different forms in various textbooks.
**Calculation Requirement:**
Use the form of the Heisenberg uncertainty relation employing:
\[
\Delta x \cdot \Delta p \geq \frac{h}{4\pi}
\]
Where:
- ∆x is the uncertainty in position (0.211 nm, as given)
- ∆p is the uncertainty in momentum
- h is Planck's constant (\(6.626 \times 10^{-34} \, \text{Js}\))
**Solution:**
To find the uncertainty in velocity (∆v), use the relationship:
\[
\Delta p = m \cdot \Delta v
\]
This leads to:
\[
\Delta x \cdot m \cdot \Delta v \geq \frac{h}{4\pi}
\]
Therefore,
\[
\Delta v \geq \frac{h}{4\pi \cdot m \cdot \Delta x}
\]
**Box for Solution:**
\[
\Delta v = \text{(Insert calculated result here)} \, \text{m/s}
\]](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F76884ef0-0050-4a4d-a83f-5c6d84fc3fcd%2Feaa922e4-7f3a-4ec9-9eb1-fec2766cd176%2Fhlx7ctf_processed.jpeg&w=3840&q=75)
Transcribed Image Text:### Understanding the Heisenberg Uncertainty Principle
**Problem Statement:**
An electron is located within an interval of 0.211 nm in the north-south direction. What is the minimum uncertainty (∆v) in the electron's velocity in that direction?
**Concept Explanation:**
The Heisenberg Uncertainty Principle is a fundamental theory in quantum mechanics that states that it is impossible to simultaneously know both the position and the velocity of a particle with absolute certainty. This principle is expressed in different forms in various textbooks.
**Calculation Requirement:**
Use the form of the Heisenberg uncertainty relation employing:
\[
\Delta x \cdot \Delta p \geq \frac{h}{4\pi}
\]
Where:
- ∆x is the uncertainty in position (0.211 nm, as given)
- ∆p is the uncertainty in momentum
- h is Planck's constant (\(6.626 \times 10^{-34} \, \text{Js}\))
**Solution:**
To find the uncertainty in velocity (∆v), use the relationship:
\[
\Delta p = m \cdot \Delta v
\]
This leads to:
\[
\Delta x \cdot m \cdot \Delta v \geq \frac{h}{4\pi}
\]
Therefore,
\[
\Delta v \geq \frac{h}{4\pi \cdot m \cdot \Delta x}
\]
**Box for Solution:**
\[
\Delta v = \text{(Insert calculated result here)} \, \text{m/s}
\]
Expert Solution
Step 1
Step by step
Solved in 2 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, chemistry and related others by exploring similar questions and additional content below.Recommended textbooks for you

Chemistry
Chemistry
ISBN:
9781305957404
Author:
Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCoste
Publisher:
Cengage Learning

Chemistry
Chemistry
ISBN:
9781259911156
Author:
Raymond Chang Dr., Jason Overby Professor
Publisher:
McGraw-Hill Education

Principles of Instrumental Analysis
Chemistry
ISBN:
9781305577213
Author:
Douglas A. Skoog, F. James Holler, Stanley R. Crouch
Publisher:
Cengage Learning

Chemistry
Chemistry
ISBN:
9781305957404
Author:
Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCoste
Publisher:
Cengage Learning

Chemistry
Chemistry
ISBN:
9781259911156
Author:
Raymond Chang Dr., Jason Overby Professor
Publisher:
McGraw-Hill Education

Principles of Instrumental Analysis
Chemistry
ISBN:
9781305577213
Author:
Douglas A. Skoog, F. James Holler, Stanley R. Crouch
Publisher:
Cengage Learning

Organic Chemistry
Chemistry
ISBN:
9780078021558
Author:
Janice Gorzynski Smith Dr.
Publisher:
McGraw-Hill Education

Chemistry: Principles and Reactions
Chemistry
ISBN:
9781305079373
Author:
William L. Masterton, Cecile N. Hurley
Publisher:
Cengage Learning

Elementary Principles of Chemical Processes, Bind…
Chemistry
ISBN:
9781118431221
Author:
Richard M. Felder, Ronald W. Rousseau, Lisa G. Bullard
Publisher:
WILEY