Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
Related questions
Question
tan A = ______
I also need to know how you got the answer.
![**Using Figure 1 to Evaluate Trigonometric Functions**
In this example, we will evaluate a trigonometric function using a right triangle as depicted in Figure 1.
**Figure 1: Right Triangle Description**
Figure 1 is a right triangle, labeled as triangle \( \triangle ABC \).
- The right angle is located at point \( C \).
- Side \( BC \) is the adjacent side to angle \( A \) and measures 16 units.
- Side \( AC \) is the opposite side to angle \( A \) and measures 4 units.
To find the length of the hypotenuse \( AB \), we can use the Pythagorean theorem:
\[ AB = \sqrt{AC^2 + BC^2} = \sqrt{4^2 + 16^2} = \sqrt{16 + 256} = \sqrt{272} = 4\sqrt{17}. \]
**Evaluating Trigonometric Functions**
Assume we want to find \(\sin A\), \(\cos A\), and \(\tan A\):
- \(\sin A = \frac{\text{opposite}}{\text{hypotenuse}} = \frac{4}{4\sqrt{17}}\).
- \(\cos A = \frac{\text{adjacent}}{\text{hypotenuse}} = \frac{16}{4\sqrt{17}}\).
- \(\tan A = \frac{\text{opposite}}{\text{adjacent}} = \frac{4}{16} = \frac{1}{4}\).
**Note:** Remember to simplify the trigonometric values where applicable. Enter the exact answer as required.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F0fb6fbe8-c93b-4e2e-8100-eedf21471e21%2Fa1a0c489-bf0b-4145-9fc8-54c0218f4b11%2F8s1ipf8_processed.png&w=3840&q=75)
Transcribed Image Text:**Using Figure 1 to Evaluate Trigonometric Functions**
In this example, we will evaluate a trigonometric function using a right triangle as depicted in Figure 1.
**Figure 1: Right Triangle Description**
Figure 1 is a right triangle, labeled as triangle \( \triangle ABC \).
- The right angle is located at point \( C \).
- Side \( BC \) is the adjacent side to angle \( A \) and measures 16 units.
- Side \( AC \) is the opposite side to angle \( A \) and measures 4 units.
To find the length of the hypotenuse \( AB \), we can use the Pythagorean theorem:
\[ AB = \sqrt{AC^2 + BC^2} = \sqrt{4^2 + 16^2} = \sqrt{16 + 256} = \sqrt{272} = 4\sqrt{17}. \]
**Evaluating Trigonometric Functions**
Assume we want to find \(\sin A\), \(\cos A\), and \(\tan A\):
- \(\sin A = \frac{\text{opposite}}{\text{hypotenuse}} = \frac{4}{4\sqrt{17}}\).
- \(\cos A = \frac{\text{adjacent}}{\text{hypotenuse}} = \frac{16}{4\sqrt{17}}\).
- \(\tan A = \frac{\text{opposite}}{\text{adjacent}} = \frac{4}{16} = \frac{1}{4}\).
**Note:** Remember to simplify the trigonometric values where applicable. Enter the exact answer as required.
Expert Solution
Step 1
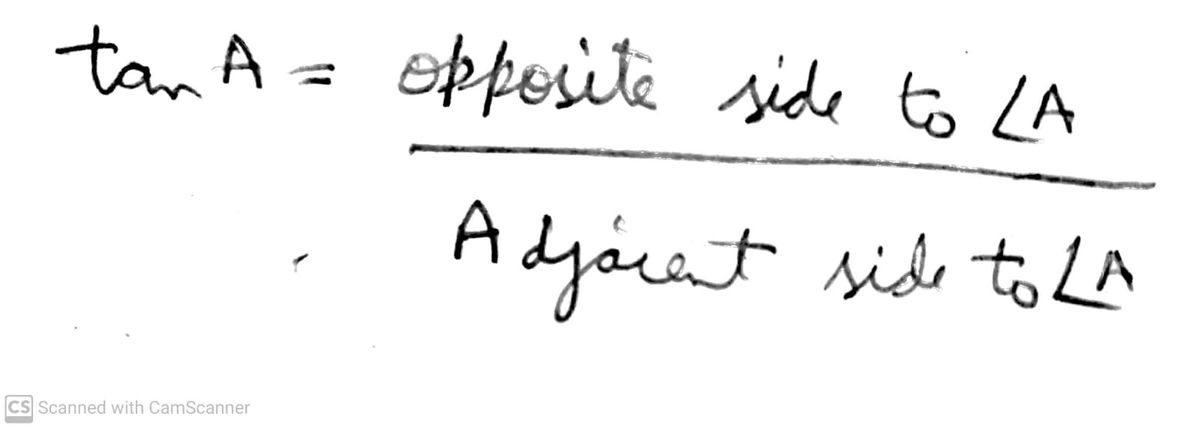
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning