### Problem Statement 1. An object is thrown upward at a speed of 183 feet per second by a machine from a height of 12 feet off the ground. The height of the object after \( t \) seconds can be found using the equation: \[ h(t) = -16t^2 + 183t + 12 \] Use the graph of this function to answer the following questions. - Round answers to the nearest hundredth, if needed. - Include units in your answers. ### Questions a) When will the object hit the ground? b) What is the maximum height of the object? c) When will the object reach its maximum height? d) When will the object reach 400 feet? e) Explain how you could find from the graph the height of the object after 2 seconds. Give an estimate of the height. ### Graph Explanation The graph represents the quadratic function \( h(t) = -16t^2 + 183t + 12 \). It is a parabola opening downwards indicating the height of an object over time. The x-axis represents time \( t \) in seconds, and the y-axis represents height \( h(t) \) in feet. - The graph shows a maximum point labeled (5.719, 535.266), indicating that the maximum height of the object is approximately 535.27 feet. - The endpoints where the graph intersects the x-axis are approximately (0.12, 0) and (11.503, 0). This indicates the times when the object is at ground level. - The object reaches the height of 400 feet at two points: (2.811, 400) and (8.626, 400). ### Answers a) The object hits the ground at approximately \( t = 11.50 \) seconds. b) The maximum height of the object is approximately 535.27 feet. c) The object reaches its maximum height at approximately \( t = 5.72 \) seconds. d) The object reaches a height of 400 feet at approximately \( t = 2.81 \) seconds and \( t = 8.63 \) seconds. e) To find the height of the object after 2 seconds, locate \( t = 2 \) on the x-axis and find the corresponding point on the graph. Estimate the y-value from the graph at
### Problem Statement 1. An object is thrown upward at a speed of 183 feet per second by a machine from a height of 12 feet off the ground. The height of the object after \( t \) seconds can be found using the equation: \[ h(t) = -16t^2 + 183t + 12 \] Use the graph of this function to answer the following questions. - Round answers to the nearest hundredth, if needed. - Include units in your answers. ### Questions a) When will the object hit the ground? b) What is the maximum height of the object? c) When will the object reach its maximum height? d) When will the object reach 400 feet? e) Explain how you could find from the graph the height of the object after 2 seconds. Give an estimate of the height. ### Graph Explanation The graph represents the quadratic function \( h(t) = -16t^2 + 183t + 12 \). It is a parabola opening downwards indicating the height of an object over time. The x-axis represents time \( t \) in seconds, and the y-axis represents height \( h(t) \) in feet. - The graph shows a maximum point labeled (5.719, 535.266), indicating that the maximum height of the object is approximately 535.27 feet. - The endpoints where the graph intersects the x-axis are approximately (0.12, 0) and (11.503, 0). This indicates the times when the object is at ground level. - The object reaches the height of 400 feet at two points: (2.811, 400) and (8.626, 400). ### Answers a) The object hits the ground at approximately \( t = 11.50 \) seconds. b) The maximum height of the object is approximately 535.27 feet. c) The object reaches its maximum height at approximately \( t = 5.72 \) seconds. d) The object reaches a height of 400 feet at approximately \( t = 2.81 \) seconds and \( t = 8.63 \) seconds. e) To find the height of the object after 2 seconds, locate \( t = 2 \) on the x-axis and find the corresponding point on the graph. Estimate the y-value from the graph at
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
![### Problem Statement
1. An object is thrown upward at a speed of 183 feet per second by a machine from a height of 12 feet off the ground. The height of the object after \( t \) seconds can be found using the equation:
\[
h(t) = -16t^2 + 183t + 12
\]
Use the graph of this function to answer the following questions.
- Round answers to the nearest hundredth, if needed.
- Include units in your answers.
### Questions
a) When will the object hit the ground?
b) What is the maximum height of the object?
c) When will the object reach its maximum height?
d) When will the object reach 400 feet?
e) Explain how you could find from the graph the height of the object after 2 seconds. Give an estimate of the height.
### Graph Explanation
The graph represents the quadratic function \( h(t) = -16t^2 + 183t + 12 \). It is a parabola opening downwards indicating the height of an object over time. The x-axis represents time \( t \) in seconds, and the y-axis represents height \( h(t) \) in feet.
- The graph shows a maximum point labeled (5.719, 535.266), indicating that the maximum height of the object is approximately 535.27 feet.
- The endpoints where the graph intersects the x-axis are approximately (0.12, 0) and (11.503, 0). This indicates the times when the object is at ground level.
- The object reaches the height of 400 feet at two points: (2.811, 400) and (8.626, 400).
### Answers
a) The object hits the ground at approximately \( t = 11.50 \) seconds.
b) The maximum height of the object is approximately 535.27 feet.
c) The object reaches its maximum height at approximately \( t = 5.72 \) seconds.
d) The object reaches a height of 400 feet at approximately \( t = 2.81 \) seconds and \( t = 8.63 \) seconds.
e) To find the height of the object after 2 seconds, locate \( t = 2 \) on the x-axis and find the corresponding point on the graph. Estimate the y-value from the graph at](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F0aec33da-7e9a-4f18-8fb9-9cc4b6ca964e%2Fdf0440b2-b8f6-443d-93a4-7ff14bf0a0ed%2Fford4dc.jpeg&w=3840&q=75)
Transcribed Image Text:### Problem Statement
1. An object is thrown upward at a speed of 183 feet per second by a machine from a height of 12 feet off the ground. The height of the object after \( t \) seconds can be found using the equation:
\[
h(t) = -16t^2 + 183t + 12
\]
Use the graph of this function to answer the following questions.
- Round answers to the nearest hundredth, if needed.
- Include units in your answers.
### Questions
a) When will the object hit the ground?
b) What is the maximum height of the object?
c) When will the object reach its maximum height?
d) When will the object reach 400 feet?
e) Explain how you could find from the graph the height of the object after 2 seconds. Give an estimate of the height.
### Graph Explanation
The graph represents the quadratic function \( h(t) = -16t^2 + 183t + 12 \). It is a parabola opening downwards indicating the height of an object over time. The x-axis represents time \( t \) in seconds, and the y-axis represents height \( h(t) \) in feet.
- The graph shows a maximum point labeled (5.719, 535.266), indicating that the maximum height of the object is approximately 535.27 feet.
- The endpoints where the graph intersects the x-axis are approximately (0.12, 0) and (11.503, 0). This indicates the times when the object is at ground level.
- The object reaches the height of 400 feet at two points: (2.811, 400) and (8.626, 400).
### Answers
a) The object hits the ground at approximately \( t = 11.50 \) seconds.
b) The maximum height of the object is approximately 535.27 feet.
c) The object reaches its maximum height at approximately \( t = 5.72 \) seconds.
d) The object reaches a height of 400 feet at approximately \( t = 2.81 \) seconds and \( t = 8.63 \) seconds.
e) To find the height of the object after 2 seconds, locate \( t = 2 \) on the x-axis and find the corresponding point on the graph. Estimate the y-value from the graph at
Expert Solution
Step 1
Since the question has multiple subparts, we will answer the first three subparts (a,b,c). If you want the remaining subparts to be answered, then please resubmit the question and mention the subparts you want us to answer in your message.
The graph of the equation is,
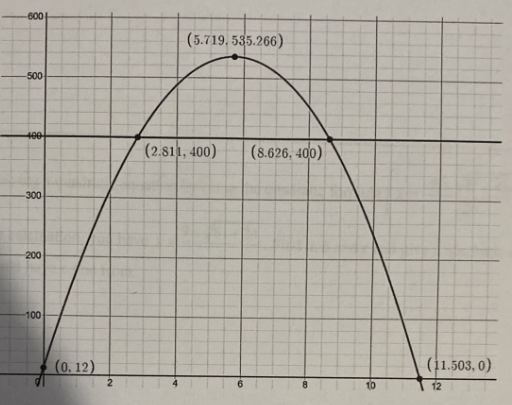
Step 2
a)
Find the time, when the object hits the ground as follows.
When the object hits the ground, the height will be zero.
So, the point that has a y coordinate of zero gives the time when object hits the ground.
From the above graph, it is observed that the point whose y coordinate is zero is .
Hence, the object hits the ground after 11.50 seconds.
Trending now
This is a popular solution!
Step by step
Solved in 4 steps with 1 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

