Advanced Math Question
Average value of a function:
Let be a function on the closed and bounded region , then the average value of the function is:
The given function is:
The given region is a triangular region with vertices and .
Draw the triangle with vertices and and identify the height and breadth of the triangle:
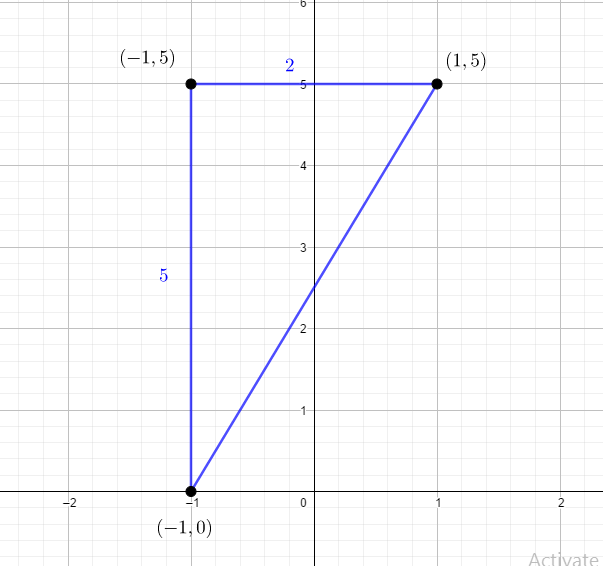Notice that the height of the triangle is and length of base of the triangle is
Formula: Area of a triangle with length of base and height is:
The length of the given triangle is and length of base of the triangle is .
The area of the triangular region is:
Formula: The equation of the line joining the two points and is:
Find the equation of the line joining the vertices and :
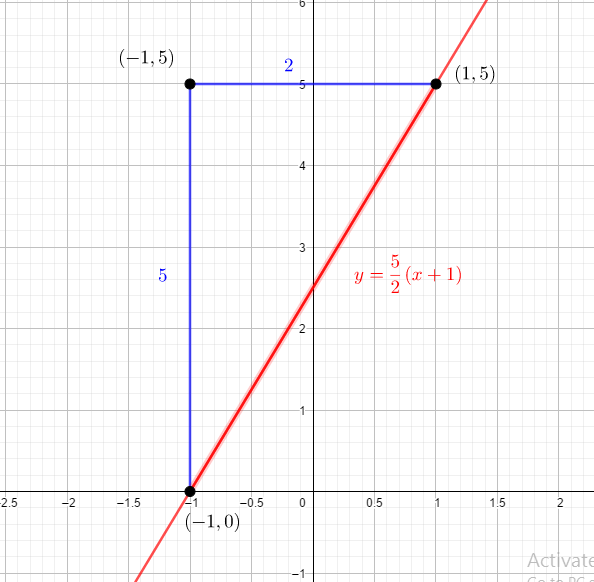
Set up limits for the double integral :
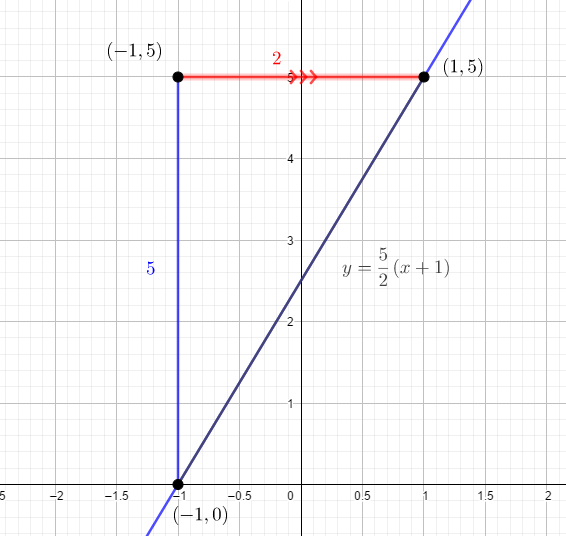Notice that in the region , the limit of changes from to .
Step by step
Solved in 9 steps with 4 images
