a=2, b=1 A bullet is to be tested in the laboratory to determine the drag force on it. Dependent parameter the drag force D (Newton) depends on the velocity of the bullet V(m/s), the length of the bullet L(m), sound velocity c(m/s), density of fluid ρ (kg/m3) and dynamic viscosity µ(kg/ms). Solve the problem by making the necessary assumptions and drawing the schematic figure I-Determine the nondimensional p parameters using repeating variables ii-a bullet with a speed of 9a,b m/s in air may be modelled in a water tunnel with a test section velocity of 2ab cm/s. Determine the length of the model, if the length of the bullet is 5a,b mm. The air and water temperature is 20 oC degree at 1 atm. iii- if the drag force on the model is measured to be 2,ab N, then determine the expected drag force on the bullet. Comment on dynamic similarity equivalence?
a=2, b=1
A bullet is to be tested in the laboratory to determine the drag force on it. Dependent parameter the drag force D (Newton) depends on the velocity of the bullet V(m/s), the length of the bullet L(m), sound velocity c(m/s), density of fluid ρ (kg/m3) and dynamic viscosity µ(kg/ms). Solve the problem by making the necessary assumptions and drawing the schematic figure
I-Determine the nondimensional p parameters using repeating variables
ii-a bullet with a speed of 9a,b m/s in air may be modelled in a water tunnel with a test section velocity of 2ab cm/s. Determine the length of the model, if the length of the bullet is 5a,b mm. The air and water temperature is 20 oC degree at 1 atm.
iii- if the drag force on the model is measured to be 2,ab N, then determine the expected drag force on the bullet. Comment on dynamic similarity equivalence?
In this problem, we have the following six variables n=6. Now, the dimension of different parameters are giving below –
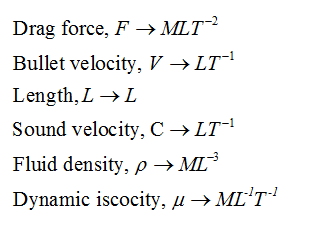
Assumptions: -
- Other variables are not affected by this phenomenon.
- Modal and prototype is considered to be similar,.
- Eddies' effects can be neglected.
We have three fundamentals quantity, m= 3
Hence the number of non-dimensional pie terms are = n – m = 6 – 3 = 3

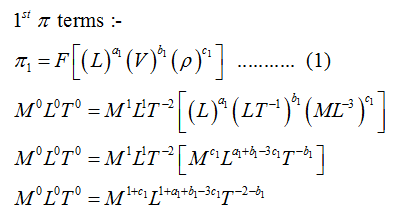
Comparing M L and T terms from both side which gives,
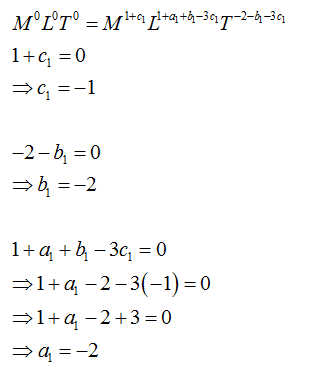
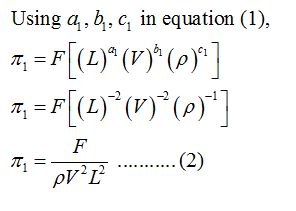
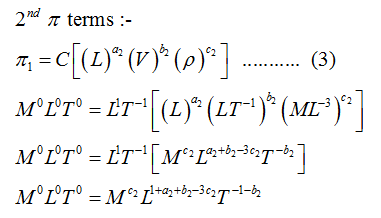
Comparing M L and T terms from both side which gives,
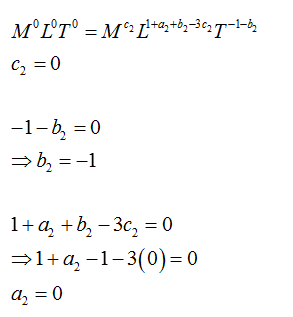
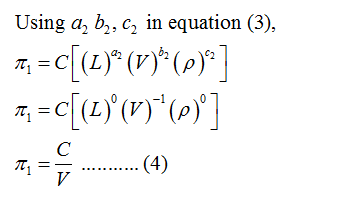
Step by step
Solved in 5 steps with 14 images









