Homework Help is Here – Start Your Trial Now!
Math
Calculus
A. Prove that if r 1 is a real number, then for all integers n ≥ 1, 1-p+1 1-r 1+r+²+. ·+p².

A. Prove that if r 1 is a real number, then for all integers n ≥ 1, 1-p+1 1-r 1+r+²+. ·+p².

Calculus: Early Transcendentals
Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
See similar textbooks
icon
Related questions
Question

Please solve the following discrete math proof 

**Mathematical Induction Example: Sum of a Geometric Series** **A. Problem Statement:** Prove that if \( r \neq 1 \) is a real number, then for all integers \( n \geq 1 \), \[ 1 + r + r^2 + \cdots + r^n = \frac{1 - r^{n+1}}{1 - r}. \] **Explanation:** This problem involves proving a formula for the sum of a geometric series with \( n+1 \) terms, starting from \( r^0 = 1 \) and ending at \( r^n \). The formula shows how to express this finite series as a simple fraction when \( r \neq 1 \). - The left side of the equation represents the sum of a series of powers of \( r \). - The right side provides a way to calculate that sum using the formula \( \frac{1 - r^{n+1}}{1 - r} \). This is a classic example of using a mathematical formula to simplify the process of summing a series, and it's often proven using mathematical induction.
Transcribed Image Text:**Mathematical Induction Example: Sum of a Geometric Series** **A. Problem Statement:** Prove that if \( r \neq 1 \) is a real number, then for all integers \( n \geq 1 \), \[ 1 + r + r^2 + \cdots + r^n = \frac{1 - r^{n+1}}{1 - r}. \] **Explanation:** This problem involves proving a formula for the sum of a geometric series with \( n+1 \) terms, starting from \( r^0 = 1 \) and ending at \( r^n \). The formula shows how to express this finite series as a simple fraction when \( r \neq 1 \). - The left side of the equation represents the sum of a series of powers of \( r \). - The right side provides a way to calculate that sum using the formula \( \frac{1 - r^{n+1}}{1 - r} \). This is a classic example of using a mathematical formula to simplify the process of summing a series, and it's often proven using mathematical induction.
Expert Solution
Step 1: Define the problem

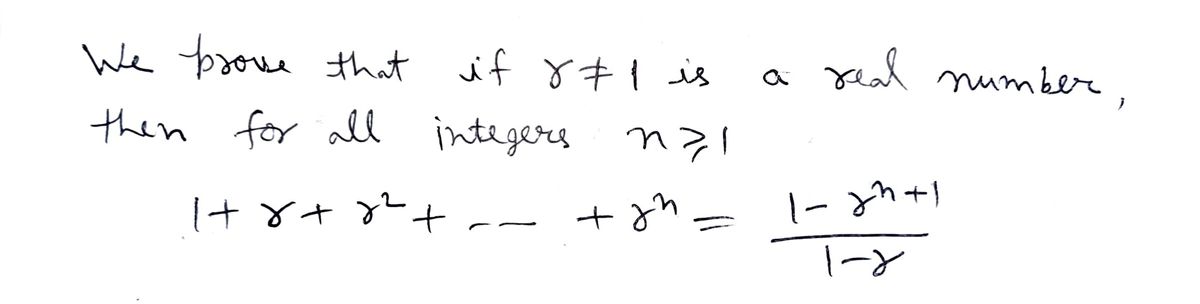
Calculus homework question answer, step 1, image 1

steps

Step by step

Solved in 3 steps with 3 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Recommended textbooks for you
Calculus: Early Transcendentals
Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning
Thomas' Calculus (14th Edition)
Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON
Calculus: Early Transcendentals (3rd Edition)
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON
Calculus: Early Transcendentals
Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman
Precalculus
Precalculus
Calculus
ISBN:
9780135189405
Author:
Michael Sullivan
Publisher:
PEARSON
Calculus: Early Transcendental Functions
Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning
SEE MORE TEXTBOOKS