(a) Use the Integral Test to show that the series Σ=1 (b) Find the value of the approximation s5 = Ek-12k (3) use S5 = converges. Hint: use integration by parts. (c) The Remainder Estimate for the Integral Test states that the nth remainder R₂ satisfies n+1 f(x) dx ≤ R₂ ≤ f(x) dx. Use this, along with your work in part (a), to find lower and upper bounds on the 5th remainder R5 when we - Σ Σ=1 ¹(3). Give four decimal places. k=1k to four decimal places. to approximate the value of the series s =
(a) Use the Integral Test to show that the series Σ=1 (b) Find the value of the approximation s5 = Ek-12k (3) use S5 = converges. Hint: use integration by parts. (c) The Remainder Estimate for the Integral Test states that the nth remainder R₂ satisfies n+1 f(x) dx ≤ R₂ ≤ f(x) dx. Use this, along with your work in part (a), to find lower and upper bounds on the 5th remainder R5 when we - Σ Σ=1 ¹(3). Give four decimal places. k=1k to four decimal places. to approximate the value of the series s =
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
Please use the information from part A to solve for part C.

Transcribed Image Text:(a) Use the Integral Test to show that the series Σ=1
(b) Find the value of the approximation s5 = Ek-12k
(3)
use S5 =
converges. Hint: use integration by parts.
(c) The Remainder Estimate for the Integral Test states that the nth remainder R₂ satisfies
n+1 f(x) dx ≤ R₂ ≤ f(x) dx.
Use this, along with your work in part (a), to find lower and upper bounds on the 5th remainder R5 when we
- Σ
Σ=1 ¹(3). Give four decimal places.
k=1k
to four decimal places.
to approximate the value of the series s =
![a. Ev-₁ (²)
15 e* x² dx → Sudv=uv-√fvdu
ex
-x³²e²x - √-ex• 2x dx]₁
(= 4/²x² + f(x) = ²
=
2
-X²c^² + 2√xe*dx] + Integrate Again > U=x, dvsex
-xe-* -S-e^² dx + - XX-C
ед-а-ае17
e²-¹²-2-2 e²^²^² + e²^²^² + 4e²^² = 5e²^² + 5 /e thus converges
e-2
Se
e² + 4e² = 96² +16² +25
es
b. 50 ≤²M=15²²; 2², â‚ ð , a
3
U= x² dv=e-x
du = 2x dx v=-ex
xe để xe
= 1.8188
-X](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F91706ec3-204f-4b92-a9ab-c0192b0d1542%2F17610c4b-d37e-404b-a660-db54d795c924%2Fuze1lny_processed.jpeg&w=3840&q=75)
Transcribed Image Text:a. Ev-₁ (²)
15 e* x² dx → Sudv=uv-√fvdu
ex
-x³²e²x - √-ex• 2x dx]₁
(= 4/²x² + f(x) = ²
=
2
-X²c^² + 2√xe*dx] + Integrate Again > U=x, dvsex
-xe-* -S-e^² dx + - XX-C
ед-а-ае17
e²-¹²-2-2 e²^²^² + e²^²^² + 4e²^² = 5e²^² + 5 /e thus converges
e-2
Se
e² + 4e² = 96² +16² +25
es
b. 50 ≤²M=15²²; 2², â‚ ð , a
3
U= x² dv=e-x
du = 2x dx v=-ex
xe để xe
= 1.8188
-X
Expert Solution
Step 1
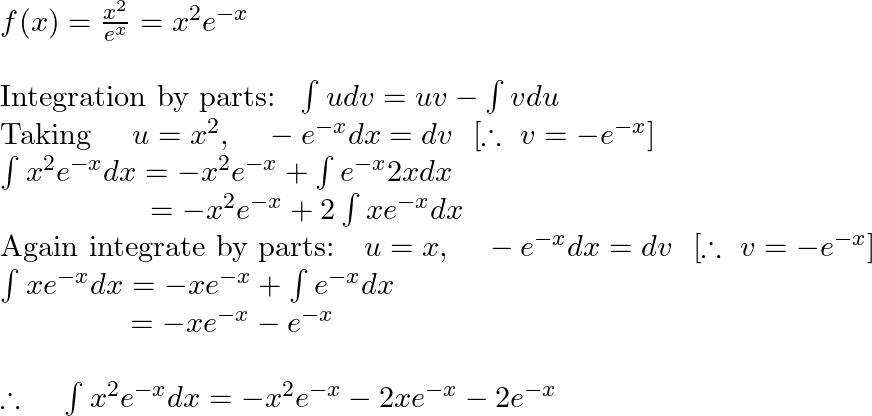
Step by step
Solved in 2 steps with 2 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

