A small pump is used to pump ambient air at 20°C into a 0.10 m³ tank at a constant volumetric flow rate of Q = 0.10 m³/min. The tank pressure is initially at 1 atm. Determine the time required to raise the pressure in the tank to 10 atm. Assume the gas in the tank remains at a constant temperature of 20°C.
So the problem is an Unsteady-State Mass Conservation problem? My professor only taught us how to do steady state where accumulation is zero, so I dont know what to do.

Given: Volumetric flow rate of air Q = 0.10 m3/min
Tank Volume V = 0.10 m3
The temperature of air entering and tank T = 20°C = 293.15 K
Initial Pressure P1 = 1 atm
Final Pressure P2 = 10 atm
To determine, the time required to raise the pressure t =?
Schematic for the given problem can be shown as below: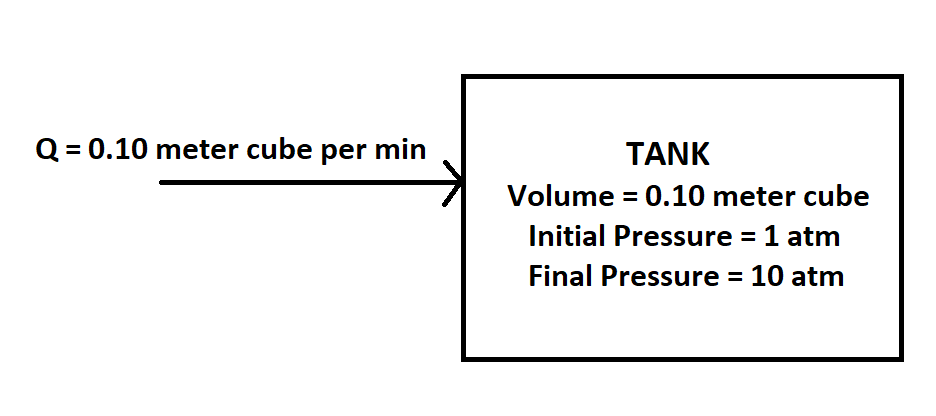
Please note that the final volume of gas inside the tank would be equal to tank volume, at higher pressure. Hence the initial and final volume in the tank is the same. Please don't confuse as more flow in coming in, the volume should be high, as additional volume is utilized in increasing the pressure of the tank.
Here we will first find out the difference in moles of initially in the tank (ni) and finally in the tank (nf).
From ideal gas law, we know:
Now, assuming the flow coming in at 1 atm, and as given at 20°C
Total volume of gas entered to change the number of moles inside would be as below:
Step by step
Solved in 3 steps with 1 images









