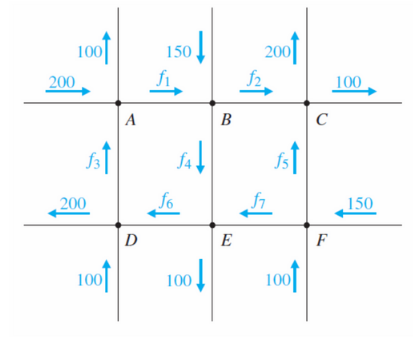
(a) Set up and solve a system of linear equations to find the possible flows in the network shown in the figure. (Use the parameterss and t as necessary.) (f,, f2, f3, fa, fs, foi fy) = ( s, 50 +t, s – 100, 100 + s – t, 250 – t, s, t (b) Is it possible for f, = 130 and f = 140? [Answer this question first with reference to your solution in part (a) and then directly from the figure.] O It is possible for f, = 130 and f = 140. O It is not possible for f, = 130 and f = 140. (c) If f, = 0, what will the range of flow be on each of the other branches? (Enter your answers using interval notation.) , range of flow f, range of flow 150 +s 3 range of flow s – 100 fs range of flow 150 – s 6 range of flow f, range of flow 100 + s
(a) Set up and solve a system of linear equations to find the possible flows in the network shown in the figure. (Use the parameterss and t as necessary.) (f,, f2, f3, fa, fs, foi fy) = ( s, 50 +t, s – 100, 100 + s – t, 250 – t, s, t (b) Is it possible for f, = 130 and f = 140? [Answer this question first with reference to your solution in part (a) and then directly from the figure.] O It is possible for f, = 130 and f = 140. O It is not possible for f, = 130 and f = 140. (c) If f, = 0, what will the range of flow be on each of the other branches? (Enter your answers using interval notation.) , range of flow f, range of flow 150 +s 3 range of flow s – 100 fs range of flow 150 – s 6 range of flow f, range of flow 100 + s
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
I get how to the rest of the problem, but for the last part of the question, i have no clue how you would write your answer in interval notation. Please help me, thank you.
![Consider the following figure.
1001
fi
150
200
200
100
A
C
f3
f4.
fs
200
150
D
E
F
1001
100
1001
(a) Set up and solve a system of linear equations to find the possible flows in the network shown in the figure. (Use the parameters s and t as necessary.)
(f,, f2, f3, fa, fs, fg, f7) = ( s, 50 +t, s – 100, 100 + s – t, 250 – t, s, t
(b) Is it possible for f, = 130 and f.
= 140? [Answer this question first with reference to your solution in part (a) and then directly from the figure.]
B.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F10a535cf-9a86-4d0d-a3ea-ce5b4c2d5fd4%2F24735f96-48d2-4eef-b6f1-a505dc5fa5b0%2Fm38anc9_processed.png&w=3840&q=75)
Transcribed Image Text:Consider the following figure.
1001
fi
150
200
200
100
A
C
f3
f4.
fs
200
150
D
E
F
1001
100
1001
(a) Set up and solve a system of linear equations to find the possible flows in the network shown in the figure. (Use the parameters s and t as necessary.)
(f,, f2, f3, fa, fs, fg, f7) = ( s, 50 +t, s – 100, 100 + s – t, 250 – t, s, t
(b) Is it possible for f, = 130 and f.
= 140? [Answer this question first with reference to your solution in part (a) and then directly from the figure.]
B.
![(a) Set up and solve a system of linear equations to find the possible flows in the network shown in the figure. (Use the parameters s and t as necessary.)
(f,, f2, f31 f4, f5, for f;) = ( s, 50 +t, s – 100, 100 + s – t, 250 – t, s, t
(b) Is it possible for f,
= 130 and f.
= 140? [Answer this question first with reference to your solution in part (a) and then directly from the figure.]
It is possible for f,
= 130 and f. = 140.
It is not possible for f,
= 130 and fs
= 140.
calcPad
Operations
(0)
[0]
Functions
(c)
If f, = 0, what will the range of flow be on each of the other branches? (Enter your answers using interval notation.)
Symbols
(0]
Relations
, range of flow
Sets
Vectors
f, range of flow
150 + s
U
Trig
Greek
fz range of flow
s – 100
O Help
f5 range of flow
150 – s
f, range of flow
S
f, range of flow
100 + s](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F10a535cf-9a86-4d0d-a3ea-ce5b4c2d5fd4%2F24735f96-48d2-4eef-b6f1-a505dc5fa5b0%2For4y4e9_processed.png&w=3840&q=75)
Transcribed Image Text:(a) Set up and solve a system of linear equations to find the possible flows in the network shown in the figure. (Use the parameters s and t as necessary.)
(f,, f2, f31 f4, f5, for f;) = ( s, 50 +t, s – 100, 100 + s – t, 250 – t, s, t
(b) Is it possible for f,
= 130 and f.
= 140? [Answer this question first with reference to your solution in part (a) and then directly from the figure.]
It is possible for f,
= 130 and f. = 140.
It is not possible for f,
= 130 and fs
= 140.
calcPad
Operations
(0)
[0]
Functions
(c)
If f, = 0, what will the range of flow be on each of the other branches? (Enter your answers using interval notation.)
Symbols
(0]
Relations
, range of flow
Sets
Vectors
f, range of flow
150 + s
U
Trig
Greek
fz range of flow
s – 100
O Help
f5 range of flow
150 – s
f, range of flow
S
f, range of flow
100 + s
Expert Solution
Step 1
Note: As you have asked for only for the last question. We are going to solve that only with the help of the given solution.
The given figure is:
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 1 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

