Consider the second order equation below. Find a recursion equation for the coefficients of the pow series solution. Express the coefficient an+1 in terms of n and an. −2xy"+(2x − 3)y'+5y = 0 [Note: complete the recursion equation by only entering the function in n that is multiplied by an produce an+1 for all n ≥ 0.] an+1 = ·an; n ≥0
Consider the second order equation below. Find a recursion equation for the coefficients of the pow series solution. Express the coefficient an+1 in terms of n and an. −2xy"+(2x − 3)y'+5y = 0 [Note: complete the recursion equation by only entering the function in n that is multiplied by an produce an+1 for all n ≥ 0.] an+1 = ·an; n ≥0
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
![**Problem Statement:**
Consider the second order equation below. Find a recursion equation for the coefficients of the power series solution. Express the coefficient \( a_{n+1} \) in terms of \( n \) and \( a_n \).
\[
-2xy'' + (2x - 3)y' + 5y = 0
\]
**Note:** Complete the recursion equation by only entering the function in \( n \) that is multiplied by \( a_n \) to produce \( a_{n+1} \) for all \( n \geq 0 \.
\[
a_{n+1} = \boxed{\phantom{answer}} \cdot a_n; \quad n \geq 0
\]](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Feb48e445-6f22-4655-aae5-a52568300bfa%2F435c22c7-d308-4512-b3b3-712c532ee626%2Fbrg64ei_processed.png&w=3840&q=75)
Transcribed Image Text:**Problem Statement:**
Consider the second order equation below. Find a recursion equation for the coefficients of the power series solution. Express the coefficient \( a_{n+1} \) in terms of \( n \) and \( a_n \).
\[
-2xy'' + (2x - 3)y' + 5y = 0
\]
**Note:** Complete the recursion equation by only entering the function in \( n \) that is multiplied by \( a_n \) to produce \( a_{n+1} \) for all \( n \geq 0 \.
\[
a_{n+1} = \boxed{\phantom{answer}} \cdot a_n; \quad n \geq 0
\]
Expert Solution
Step 1: Given that:
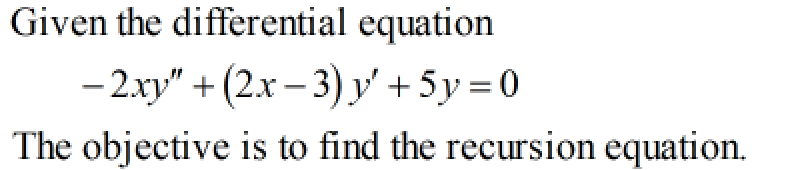
Step by step
Solved in 4 steps with 5 images

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
The question says n>0 but your solution says n>1.
Is this the correct answer for the problem ? It asks for n>0.
Solution
Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

