A publisher wants to estimate the length of time (in minutes) all adults spend reading newspapers. To determine this estimate, the publisher takes a random sample of 15 people and obtains the following results: 11, 9, 8, 10, 10, 9, 7, 11, 11, 7, 6, 9, 10, 8, 10 Assume that the population of times is normally distributed. Construct the 95% confidence interval for the mean population length reading time.
3. A publisher wants to estimate the length of time (in minutes) all adults spend reading newspapers. To determine this estimate, the publisher takes a random sample of 15 people and obtains the following results:
11, 9, 8, 10, 10, 9, 7, 11, 11, 7, 6, 9, 10, 8, 10
Assume that the population of times is
mean population length reading time.
According to given question, We have :-
data set 11, 9, 8, 10, 10, 9, 7, 11, 11, 7, 6, 9, 10, 8, 10
Sample size n= 15
Sample mean= sum/25 = 136/15 = 9.0667
Sample standard deviation s = 1.5796
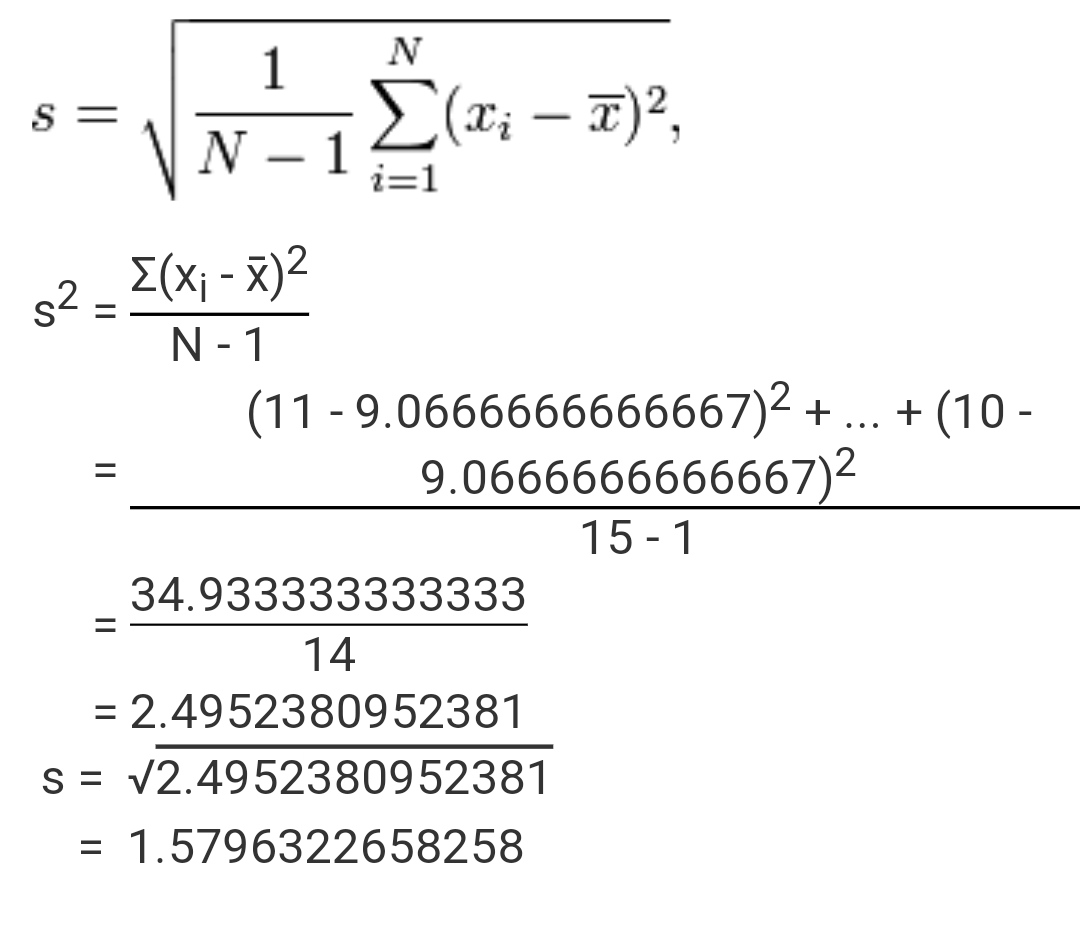
To find :-
Upper limit and lower limit of 95% confidence interval.
Formula used :- Confidence interval=point estimate ±Margin of error
where t= critical value for corresponding confidence level
s= standard deviation
n = sample size
Because population standard deviation is unknown so we use t distribution find out critical value.
Step by step
Solved in 2 steps with 2 images









