A pendulum swings back and forth from a string. When it is lying motionless it is y=6 ft from a nearby wall. When the pendulum is furthest from the wall, it is 9 ft. It takes 20 seconds to complete one cycle. Suppose you start timing the pendulum when it is furthest from the wall. a) Sketch a graph of this situation. b) Write an equation of this sinusoidal.
Q: A physical pendulum is made by cutting a circular lamina from a plywood sheet. The radius is 30 cm…
A: Given data *The mass of the sheet is m = 5 kg *The radius of the sheet is r = 30 cm = 0.30 m…
Q: wo parakeets sit on a swing with their combined CMs 10.1 cm below the pivot. At what frequency do…
A: 1. all mass is centered at 10.1 cm below the pivot. thus, it can be seen as simple pendulum of…
Q: An object with mass m is attached to a spring with stiffness k. The mass is oscillating on a smooth…
A: Oscillation is the back and forth motion of a particle in regular interval of time. Amplitude (A) of…
Q: You start a mass on a spring oscillating by pulling it down 0.10 m and releasing it. You find that…
A: It completes 2 oscillations in 1 second Time taken for 1 oscillation = 0.5 secondsSpring oscillates…
Q: 1. A2 kg mass attached to a spring with a spring constant of 400 N/m is pulled 10 cm from…
A:
Q: A spring with spring constant 11 N/m hangs from the ceiling. A ball is attached to the spring and…
A: spring constant is k= 11 N/mamplitude is A= 3.5cmnumber of oscillation = 26time taken t =19s
Q: In (Figure 1), what is the maximum speed of a 2.0 g particle that oscillates between x = 2.0 mm and…
A:
Q: A simple pendulum with mass m = 1.7 kg and length L = 2.54 m hangs from the ceiling. It is pulled…
A:
Q: Grandfather clocks are designed to have a period of exactly two seconds. Determine the following…
A: The time period of the clock is 2 s.
Q: The motion of a particle is defined by the following equations: dx dy = x – 2y and dt = 5 x – y with…
A:
Q: A 50-cm long spring is suspended from the ceiling. A 230 g mass is connected to the end held at rest…
A:
Q: A pendulum of length 1.8m with mass 2.5kg attached to its end oscillates with a period of 9.0s. What…
A:
Q: Determine the amplitude of the motion. Determine the phase constant. Determine the position of the…
A: Given-
Q: A block of mass 1.37 kg is connected to a spring of spring constant 136 N/m which is then set into…
A: Given Mass (m) = 1.37 kg Spring constant (k) = 136…
Q: Consider two pendulums with lengths /1 and l2 performing simple harmonic motion. The first pendulum…
A: In this question we have to answer how to find the ratio of the lengths of different pendulums i.e.…
Q: Consider two pendulums with lengths l1 and I2 performing simple harmonic motion. The first pendulum…
A: Given : Two pendulums performing simple harmonic motion. First one have a rate of oscillation 10…
Q: A spring scale at the grocery store reads 19N. Sean discovers that the pan goes down 8.0cm when he…
A: Given data: The force is F=19 N The displacement is x=8 cm The following is the picture of the…
Q: buoy in the ocean oscillates up and down in simple harmonic motion according to the equation y =…
A: buoy in the ocean oscillates up and down in simple harmonic motion according to the equation y =…
Q: The common field cricket makes its characteristic loud chirping sound using a specialized vibrating…
A: In the given plot for intensity versus time, there are about 31 maxima and 30 minima. Thus, there…
Q: An object stretches a spring 6 inches in equilibrium. a) Find its displacement for t> 0 if it is…
A:
Q: A mass M is connected to a spring and can slide horizontally without friction. Stretching the spring…
A: As per our guidelines, we are supposed to answer only first three subparts in case of multiple…
Q: 2. A 0.85kg block on a spring is oscillating with an amplitude of A = 0.42m and a frequency of f =…
A: Given data: Mass of the block, m=0.85 kg Amplitude of the block, A=0.42 m Frequency of oscillation,…
Q: .An object moves in simple harmonic motion described by d = 6 cos 1, where t is measured in seconds…
A: Given data Distance, d = 6cos3π2t
Q: You want to use a pendulum clock on the moon (gm= 1.625m/s2) a) What length should the pendulum…
A:
Q: 2. Jack and Jill are playing with a tire swing tied to a tree branch. Jack is standing on one side…
A: SOlution: To find the numbe rof oscillations for the tire being oscillated.
Q: A mass m = 2.5 kg is connected to a spring. The mass is pulled back a distance Ax = 0.20 m to the…
A: Since you have posted a question with a multiple sub parts, we will solve first three sub - parts…
Q: A spring is hung from the ceiling, when a block is attached to its end, it stretches 3.0 cm before…
A:
Q: A weight is suspended from a spring and is moving up and down in a simple harmonic motion. At start,…
A: Concept: The rest position of the mass attached to the spring is the equilibrium point of…
Q: Can someone help me? I am very confused with this question. What would the general shape of a…
A:
Q: A mass is attached to the end of a spring and set into oscillation on a horizontal frictionless…
A:
A pendulum swings back and forth from a string. When it is lying motionless it is y=6 ft from a nearby wall. When the pendulum is furthest from the wall, it is 9 ft. It takes 20 seconds to complete one cycle. Suppose you start timing the pendulum when it is furthest from the wall.
a) Sketch a graph of this situation.
b) Write an equation of this sinusoidal.
The diagram which represents above problem is shown in the fig below:
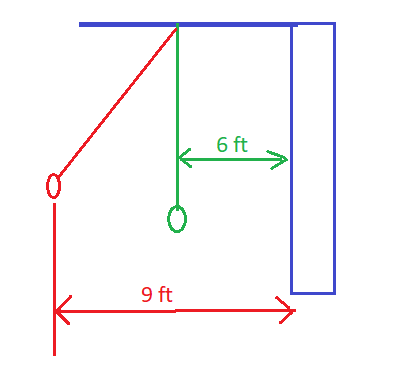
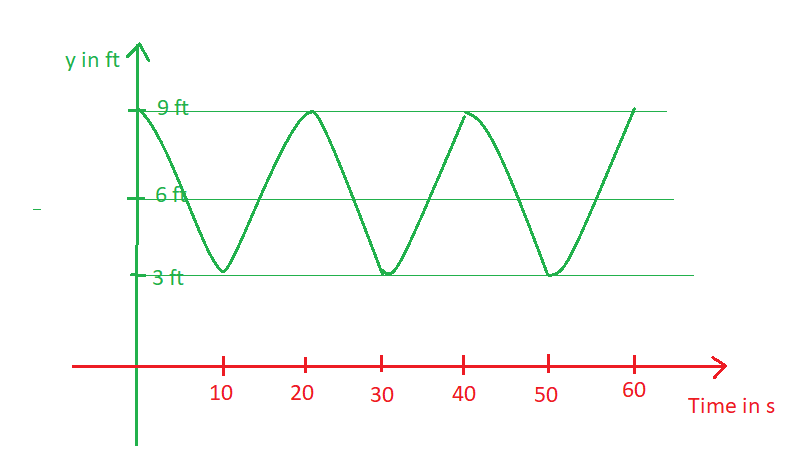
At the mean position, y=6 ft, and at the extreme position y=9 ft. So that the amplitude of the motion is 3 ft. Also given that the time period of the motion is 20 s. The graph of this oscillation is shown below:
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 2 images

- Near the top of the Citigroup Center building in New York City, there is an object with mass of 3.2 × 105 kg on springs that have adjustable force constants. Its function is to dampen wind-driven oscillations of the building by oscillating at the same frequency as the building is being driven—the driving force is transferred to the object, which oscillates instead of the entire building. A. What effective spring constant should the springs have to make them oscillate with a period of 2.2 s in N/m? B. What energy is stored in the springs for a 1.4 m displacement from equilibrium in J?A mass of 0.407 kilograms is oscillating horizontally on a spring. Its position is given by the equation x = [0.108 sin (9.24t + 0.82) + 0.683] m. a. What is the spring constant of the spring? Include units in your answer. More information. b. The velocity of the mass is another sinusoid, which also can be modeled using the equation v = [A sin (Bt + C) + D] m/s. What are those values? Do not bother with units.A: B: C: (between 0 and 2?)D: c. The acceleration of the mass is yet another sinusoid, which again can be modeled using the equation a = [A sin (Bt + C) + D] m/s/s. What are those values of A and C? Do not bother with units. Hint: For A, consider Newton's second law of motion.A: C: (between 0 and 2?)Note that the values of B and D for the acceleration equation are the same as the values of B and D for the velocity equation.Questions 6-13 refer to the figure below. The graph represents the position as a function of time for a small 1.20 kg object attached to a light spring that is oscillating on a smooth horizontal surface. n 0.4 Time (s) 0 0.2 6. What is the amplitude of the motion (in cm)? 7. What is the period of the motion (in s)? 8. What is the frequency of the motion (in Hz)? 9. What is the angular frequency of the motion (in rad/s)? 0.6 11. What is the maximum speed of the object (in m/s)? 10. What is the spring constant of the spring (in N/m)? (Be aware of units!) 0.8 12. What is the maximum acceleration of the object (in m/s²)? 13. If instead of attaching the 1.20 kg mass to the spring, we attach a mass of 2.4 kg. What is the new period (in s) of the motion?
- A mass m = 3.3 kg is at the end of a horizontal spring on a frictionless horizontal surface. The mass is oscillating with an amplitude A = 4.5 cm and a frequency f = 1.5 Hz. a. Write an equation for the spring constant k. b. Calculate the spring constant k, in Newtons per meter. c. Write an equation for the total mechanical energy, E, of the motion. Your expression should be in terms of the variables in the original problem statement. d. Calculate the total mechanical energy E, in joules.4. The displacement y(t) of an undamped oscillator of mass m>0 on a spring with spring constant k>0, and initial displacement a + 0 and initial velocity zero satisfies my" + ky = 0, y(0) = a, y'(0) = 0 %3D a. Solve this initial value problem. b. Show that the solution is periodic with period T, meaning that y(t+T)= y(t), and express Tin terms of m and k.1. A pendulum with mass 2kg, length 2.5m swings with amplitude A = 2cm. After a long time the amplitude decreases to 1 cm due to air drag. How long is the period after the amplitude decrease? 2. What is the period of oscillation of the pendulum before and after the amplitude change?
- A pendulum makes 12 complete cycles in 20 s. What is the length of this pendulum? Select one: a. 50cm b. 60cm с. 30cm d. 40cm e. 70cmQ3, first three parts5. A "seconds pendulum" is one that moves through its equilibrium position once each second. (The period of the pendulum is precisely 2 s.) The length of a seconds pendulum is 0.992 7 m at Tokyo, Japan and 0.994 2 m at Cambridge, England. What is the ratio of the free-fall accelerations at these two locations?
- 8.1A 7.2 kg-block attached to a 32 N/m-spring constant spring moves on a frictionless horizontal surface, back and forth between -3.0 m and +3.0 m. What is the period of this motion, in seconds? Your answer needs to have 2 significant figures, including the negative sign in your answer if needed. Do not include the positive sign if the answer is positive. No unit is needed in your answer, it is already given in the question statement.A spring with spring constant 15 N/m hangs from the ceiling. A ball is attached to the spring and allowed to come to rest. It is then pulled down 9.5 cm and released. The ball makes 20 oscillations in 23 s seconds. You may want to review (Pages 403-404) Part A What is its the mass of the ball? Express your answer to two significant figures and include the appropriate units. m = Submit Part B "i Vmax= μA Submit Value Request Answer What is its maximum speed? Express your answer to two significant figures and include the appropriate units. μA Value Units Request Answer ? Units ?