A pathologist has been studying the frequency of bacterial colonies within the field of a microscope using samples of throat cultures from healthy adults. Long-term history indicates that there is an average of 2.98 bacteria colonies per field. Let r be a random variable that represents the number of
A pathologist has been studying the frequency of bacterial colonies within the field of a microscope using samples of throat cultures from healthy adults. Long-term history indicates that there is an average of 2.98 bacteria colonies per field. Let r be a random variable that represents the number of bacteria colonies per field. Let O represent the number of observed bacteria colonies per field for throat cultures from healthy adults. A random sample of 100 healthy adults gave the following information.
| r | 0 | 1 | 2 | 3 | 4 | 5 or more |
| O | 13 | 13 | 27 | 18 | 21 | 8 |
| e−??r |
| r! |
| P(0) | = |
| P(1) | = |
| P(2) | = |
| P(3) | = |
| P(4) | = |
| P(5 or more) | = |
Compute the expected number of colonies E = 100P(r) for r = 0, 1, 2, 3, 4, and 5 or more. (Round your answers to one decimal place.)
| E(0) | = |
| E(1) | = |
| E(2) | = |
| E(3) | = |
| E(4) | = |
| E(5 or more) | = |
Compute the sample statistic
|
|||
and the degrees of freedom. (Round your test statistic to three decimal places.)
| d.f. | = |
| ?2 | = |
Hello
According to Bartleby Guidelines we are supposed to answer only first three sub parts so for rest of solution kindly post it again or with specific instructions.
Thank you.
Part (a):
The probability mass function for Poisson distribution is as follows:
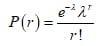
Here, λ is 2.98 it is the average number of bacteria colonies per field.
Step by step
Solved in 10 steps with 8 images









