A particle with a charge of -1.24×10-8 C is moving with instantaneous velocity Ø = (4.19x10* m/s)i +(−3.85x10* m/s).
A particle with a charge of -1.24×10-8 C is moving with instantaneous velocity Ø = (4.19x10* m/s)i +(−3.85x10* m/s).
Related questions
Question
![**Text Transcription:**
A particle with a charge of \( -1.24 \times 10^{-8} \, C \) is moving with instantaneous velocity
\[
\vec{v} = (4.19 \times 10^4 \, \text{m/s}) \hat{\imath} + (-3.85 \times 10^4 \, \text{m/s}) \hat{\jmath}.
\]
**Explanation:**
- **Charge:** The particle carries a charge of \( -1.24 \times 10^{-8} \) coulombs, indicating it is negatively charged.
- **Velocity Vector:** The velocity of the particle is expressed in vector form:
- The \( \hat{\imath} \) component (x-direction) is \( 4.19 \times 10^4 \) meters per second.
- The \( \hat{\jmath} \) component (y-direction) is \( -3.85 \times 10^4 \) meters per second.
- **Graph/Diagram:** No graphs or diagrams are provided in the image.
This information could be used to analyze the motion of charged particles in fields or to calculate resultant forces if an external field is applied.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fe5003d82-d326-4ce1-8cd1-8a5cecc2a14b%2F7e1940ee-20d2-4d54-9a2f-9c42bf575b04%2Fts9qqt_processed.png&w=3840&q=75)
Transcribed Image Text:**Text Transcription:**
A particle with a charge of \( -1.24 \times 10^{-8} \, C \) is moving with instantaneous velocity
\[
\vec{v} = (4.19 \times 10^4 \, \text{m/s}) \hat{\imath} + (-3.85 \times 10^4 \, \text{m/s}) \hat{\jmath}.
\]
**Explanation:**
- **Charge:** The particle carries a charge of \( -1.24 \times 10^{-8} \) coulombs, indicating it is negatively charged.
- **Velocity Vector:** The velocity of the particle is expressed in vector form:
- The \( \hat{\imath} \) component (x-direction) is \( 4.19 \times 10^4 \) meters per second.
- The \( \hat{\jmath} \) component (y-direction) is \( -3.85 \times 10^4 \) meters per second.
- **Graph/Diagram:** No graphs or diagrams are provided in the image.
This information could be used to analyze the motion of charged particles in fields or to calculate resultant forces if an external field is applied.
![**Problem Statement:**
What is the force exerted on this particle by a magnetic field \(\vec{B} = (2.40 \, \text{T}) \, \hat{k}\)?
**Task:**
Express the \(x\), \(y\), and \(z\) components of the force in newtons separated by commas.
---
**Explanation:**
In this problem, we are asked to determine the components of the force exerted on a particle when it is subjected to a magnetic field directed along the \(z\)-axis, given as \(\vec{B} = (2.40 \, \text{T}) \, \hat{k}\). The solution requires applying principles from electromagnetism, specifically the Lorentz force equation for a charged particle moving in a magnetic field:
\[
\vec{F} = q (\vec{v} \times \vec{B})
\]
Here, \(\vec{F}\) is the force, \(q\) is the charge of the particle, \(\vec{v}\) is the velocity of the particle, and \(\vec{B}\) is the magnetic field. The task is to calculate and express the components of \(\vec{F}\) in the \(x\), \(y\), and \(z\) directions.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fe5003d82-d326-4ce1-8cd1-8a5cecc2a14b%2F7e1940ee-20d2-4d54-9a2f-9c42bf575b04%2Fforj3dt_processed.png&w=3840&q=75)
Transcribed Image Text:**Problem Statement:**
What is the force exerted on this particle by a magnetic field \(\vec{B} = (2.40 \, \text{T}) \, \hat{k}\)?
**Task:**
Express the \(x\), \(y\), and \(z\) components of the force in newtons separated by commas.
---
**Explanation:**
In this problem, we are asked to determine the components of the force exerted on a particle when it is subjected to a magnetic field directed along the \(z\)-axis, given as \(\vec{B} = (2.40 \, \text{T}) \, \hat{k}\). The solution requires applying principles from electromagnetism, specifically the Lorentz force equation for a charged particle moving in a magnetic field:
\[
\vec{F} = q (\vec{v} \times \vec{B})
\]
Here, \(\vec{F}\) is the force, \(q\) is the charge of the particle, \(\vec{v}\) is the velocity of the particle, and \(\vec{B}\) is the magnetic field. The task is to calculate and express the components of \(\vec{F}\) in the \(x\), \(y\), and \(z\) directions.
Expert Solution
Step 1
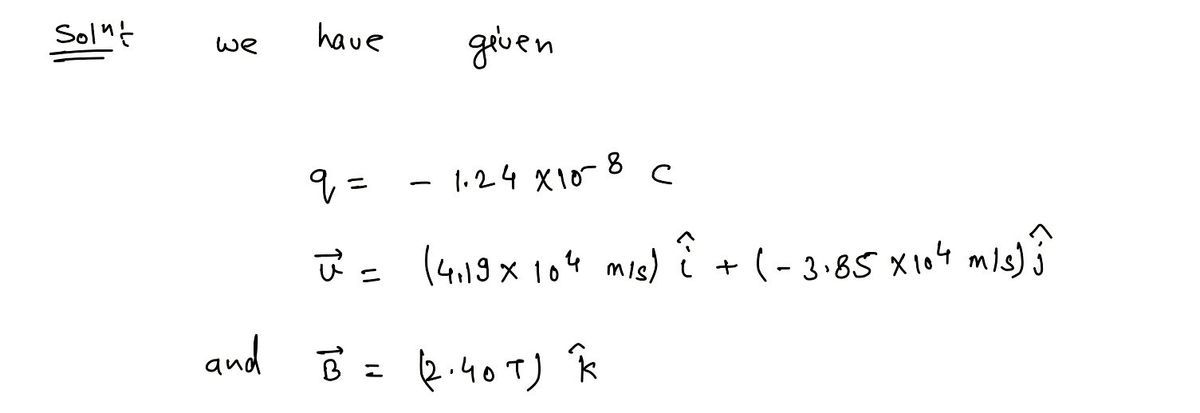
Step by step
Solved in 2 steps with 2 images
