A mortar is like a small cannon that launches shells at steep angles. A mortar crew is positioned near the top of a steep hill. Enemy forces are charging up the hill and it is necessary for the crew to spring into action. Angling the mortar at an angle of 0 = 65.0° (as shown), the crew fires the shell at a muzzle velocity of 148 ft/s. How far d down the hill does the shell strike if the hill subtends an angle p = 37.0° from the horizontal? Ignore air friction. d = m How long will the mortar shell remain in the air? time: How fast will the shell be traveling when it hits the ground? speed: m/s
A mortar is like a small cannon that launches shells at steep angles. A mortar crew is positioned near the top of a steep hill. Enemy forces are charging up the hill and it is necessary for the crew to spring into action. Angling the mortar at an angle of 0 = 65.0° (as shown), the crew fires the shell at a muzzle velocity of 148 ft/s. How far d down the hill does the shell strike if the hill subtends an angle p = 37.0° from the horizontal? Ignore air friction. d = m How long will the mortar shell remain in the air? time: How fast will the shell be traveling when it hits the ground? speed: m/s
Related questions
Question

Transcribed Image Text:A mortar is like a small cannon that launches shells at
steep angles. A mortar crew is positioned near the top of a
steep hill. Enemy forces are charging up the hill and it is
necessary for the crew to spring into action. Angling the
mortar at an angle of 0
65.0° (as shown), the crew fires
the shell at a muzzle velocity of 148 ft/s.
How far d down the hill does the shell strike if the hill
d
subtends an angle o = 37.0° from the horizontal? Ignore
air friction.
d =
How long will the mortar shell remain in the air?
time:
S
How fast will the shell be traveling when it hits
the ground?
speed:
m/s
Expert Solution
Step 1
Consider the following figure which represents the motion of the shell.
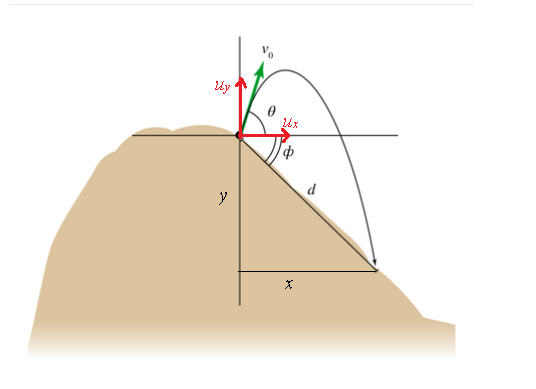
Here, y represents the vertical displacement of the shell and x represents the horizontal displacement of the shell.
According to geometry, the values of x and y are given in the following way.

The vertical and horizontal components of the initial velocity and acceleration are given in the following way.
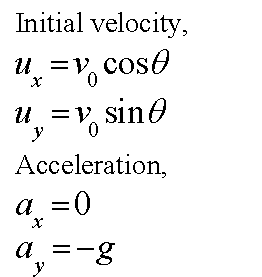
Here, g is the acceleration due to gravity.
In this case,
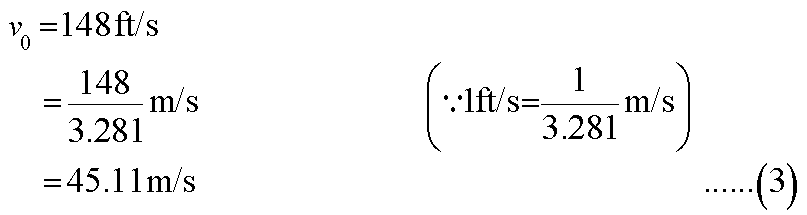
Let the time for which the shell remains in the air be t.
According to Newton’s equation of motion, the value of d in terms of t and v0 is calculated in the following way.
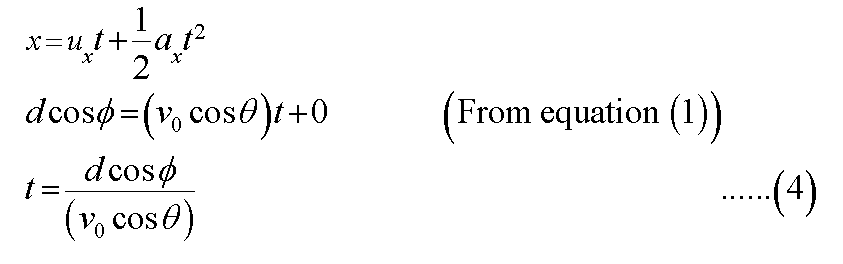
Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 11 images
