Answered: A lamina V of uniform mass density and…

Related questions

Question

A lamina V of uniform mass density and total mass M kilograms occupies the region between y = l - x 2 and the x-axis (with distance measured in meters). Calculate the rotational kinetic energy if V rotates with angular velocity w = 4 radians per second about:
(a) the x-axis. (b) the z-axis.

Expert Solution

Step 1

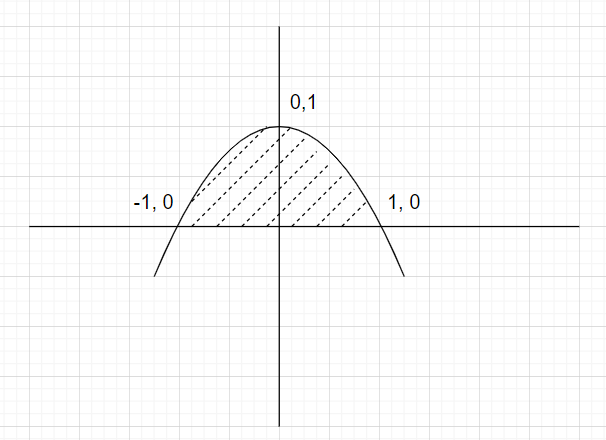
The curve $y = 1 - x^{2}$ gives a parabola with vertex at (0,1) and is downward facing. The parabola intersects the x axis at $x = \pm 1$ . The lamina $V$ is shown shaded in the figure.

Step 2

The rotational kinetic energy of a rotating object is given by,

$K E_{r o t} = \frac{1}{2} I ω^{2}$

where $I$ is the moment of inertia of the object about the rotation axis and $ω$ is its angular velocity.

Given,

Total mass of the lamina = $M k g$

Angular velocity $ω = 4 r a d s^{- 1}$

To solve this question we need to find out the moments of inertia about the axis in question.

Step 3

(a) Calculation of moment of inertia of the lamina about the x axis.

Moment of inertia is given as,

$I = \int r^{2} d m$

where $r$ is the distance of elementary mass $d m$ from the axis of rotation. In this case the axis of rotation is the x axis.

Let us define the mass per unit area of the lamina as $σ$ i.e.

$σ = \frac{M}{A}$

where $A$ is the total area of the lamina which is calculated as,

$\begin{array}{rcl} A & = & 2 \int_{0}^{1} y d x \\ = & 2 \int_{0}^{1} (1 - x^{2}) d x \\ = & 2 (1 - \frac{1}{3}) = \frac{4}{3} m^{2} \end{array}$

Thus, $σ = \frac{3 M}{4} k g m^{- 2}$

Step 4

The moment of inertia is calculated as shown in the figure below

$d m = 2 σ x d y$

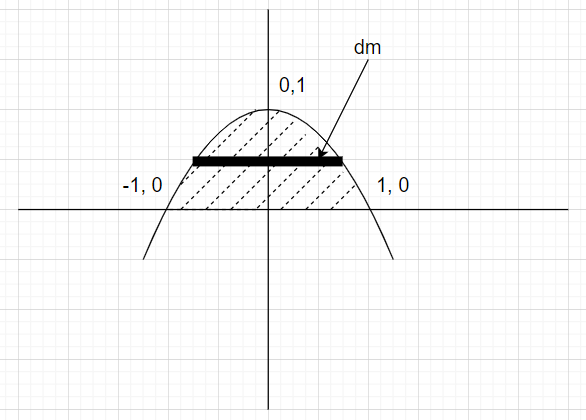
So,

$\begin{array}{rcl} d I & = & d m y^{2} \\ I & = & \int y^{2} d m \\ = & 2 \int_{0}^{1} σ x y^{2} d y \\ = & 2 σ \int_{0}^{1} y^{2} \sqrt{1 - y} d y \end{array}$

On integrating, it comes out to be,

$I_{x} = \frac{8 M}{35} k g m^{2}$

Step 5

The rotational kinetic energy of the lamina when it rotates about the x axis is,

$K E_{r o t} = \frac{1}{2} I_{x} ω^{2} = \frac{1}{2} \frac{8 M}{35} {(4)}^{2} = \frac{64 M}{35} J$

Step by step

Solved in 9 steps with 3 images

A lamina V of uniform mass density and total mass M kilograms occupies the region between y = l - x 2 and the x-axis (with distance measured in meters). Calculate the rotational kinetic energy if V rotates with angular velocity w = 4 radians per second about: (a) the x-axis. (b) the z-axis.